题目内容
【题目】如图,圆心都在x轴正半轴上的半圆O1 , 半圆O2 , …,半圆On与直线l相切.设半圆O1 , 半圆O2 , …,半圆On的半径分别是r1 , r2 , …,rn , 则当直线l与x轴所成锐角为30°,且r1=1时,r2018=.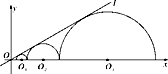
【答案】32017
【解析】分别作O1A⊥l,O2B⊥l,O3C⊥l,如图,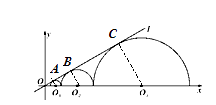
∵半圆O1 , 半圆O2 , …,半圆On与直线L相切,
∴O1A=r1 , O2B=r2 , O3C=r3 ,
∵∠AOO1=30°,
∴OO1=2O1A=2r1=2, 在Rt△OO2B中,OO2=2O2B,即2+1+r2=2r2 ,
∴r2=3, 在Rt△OO2C中,OO3=2O2C,即2+1+2×3++r3=2r3 ,
∴r3=9=32 , 同理可得r4=27=33 , 所以r2018=32017 .
故答案为32017 .
连接圆心和切点出现垂直于切线的半径,利用30度角的性质,观察规律,可看出rn=3n-1,进而求出答案.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目