题目内容
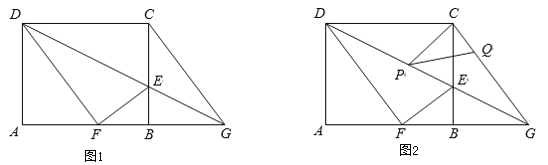
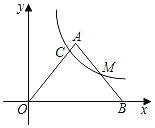
【题目】A，B是⊙C上的两个点，点P在⊙C的内部．若∠APB为直角，则称∠APB为AB关于⊙C的内直角，特别地，当圆心C在∠APB边（含顶点）上时，称∠APB为AB关于⊙C的最佳内直角．如图1，∠AMB是AB关于⊙C的内直角，∠ANB是AB关于⊙C的最佳内直角．在平面直角坐标系xOy中．
（1）如图2，⊙O的半径为5，A（0，﹣5），B（4，3）是⊙O上两点．
①已知P1（1，0），P2（0，3），P3（﹣2，1），在∠AP1B，∠AP2B，∠AP3B，中，是AB关于⊙O的内直角的是 ；
②若在直线y=2x+b上存在一点P，使得∠APB是AB关于⊙O的内直角，求b的取值范围．
（2）点E是以T（t，0）为圆心，4为半径的圆上一个动点，⊙T与x轴交于点D（点D在点T的右边）．现有点M（1，0），N（0，n），对于线段MN上每一点H，都存在点T，使∠DHE是DE关于⊙T的最佳内直角，请直接写出n的最大值，以及n取得最大值时t的取值范围．
【答案】（1）①∠AP2B，∠AP3B；②﹣5＜b≤5；（2）n的最大值为2；t的取值范围是﹣
﹣1≤t＜5
【解析】
（1）判断点P1，P2，P3是否在以AB为直径的圆弧上即可得出答案；
（2）求得直线AB的解析式，当直线y=2x+b与弧AB相切时为临界情况，证明△OAH∽△BAD，可求出此时b=5，则答案可求出；
（3）可知线段MN上任意一点（不包含点M）都必须在以TD为直径的圆上，该圆的半径为2，则当点N在该圆的最高点时，n有最大值2，再分点H不与点M重合，点M与点H重合两种情况求出临界位置时的t值即可得解．
解：（1）如图1，
，
，
，
，
，
，
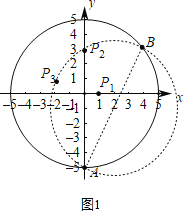
不在以
为直径的圆弧上，
故
不是关于
的内直角，
，，，
，
，
，
，
，
是关于的内直角，
同理可得，
，
是关于的内直角，
故答案为：
，
；
（2）
是关于的内直角，
，且点
在的内部，
满足条件的点形成的图形为如图2中的半圆
（点
，
均不能取到），
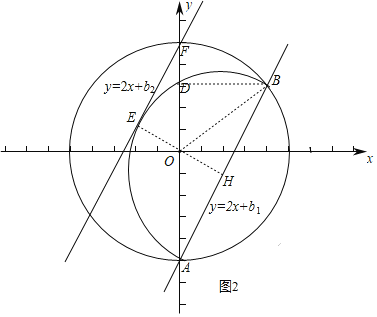
过点作
轴于点
，
，，
，
，
并可求出直线的解析式为
，
当直线
过直径时，
，
连接
，作直线
交半圆于点
，过点作直线
，交
轴于点
，
，
，
，
，
是半圆的切线．
，
，
，
，
，
，
，
，
，
，
，直线的解析式为，
直线
的解析式为
，此时
，
的取值范围是
．
（3）
对于线段
上每一个点，都存在点
，使
是
关于
的最佳内直角，
点一定在的边上，
，
，线段上任意一点（不包含点
都必须在以
为直径的圆上，该圆的半径为2，
当点
在该圆的最高点时，
有最大值，
即的最大值为2．
分两种情况：
①若点不与点
重合，那么点必须在边
上，此时，
点在以
为直径的圆上，
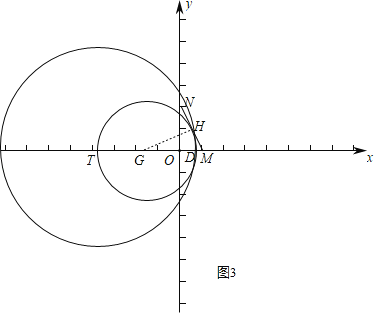
如图3，当
与相切时，
，
，
，
，
，
，
，
，
，
，
，
当与重合时，
，
此时
的取值范围是
，
②若点与点重合时，临界位置有两个，一个是当点与重合时，，另一个是当
时，
，
此时的取值范围是
，
综合以上可得，的取值范围是
．
