题目内容
【题目】在平面直角坐标系xOy中,直线x=3与直线y=![]() x+1交于点A,函数y=
x+1交于点A,函数y=![]() (k>0,x>0)的图象与直线x=3,直线y=
(k>0,x>0)的图象与直线x=3,直线y=![]() x+1分别交于点B,C.
x+1分别交于点B,C.
(1)求点A的坐标.
(2)横、纵坐标都是整数的点叫做整点.记函数y=![]() (k>0,x>0)的图象在点B,C之间的部分与线段AB,AC围成的区域(不含边界)为W.
(k>0,x>0)的图象在点B,C之间的部分与线段AB,AC围成的区域(不含边界)为W.
①当k=1时,结合函数图象,求区域W内整点的个数;
②若区域W内恰有1个整点,直接写出k的取值范围.
【答案】(1)A(3,![]() );(2)①在W区域内有1个整数点;②当区域W内恰有1个整点时,1≤k<2或16<k≤20
);(2)①在W区域内有1个整数点;②当区域W内恰有1个整点时,1≤k<2或16<k≤20
【解析】
(1)根据题意列方程即可得到结论;
(2)①当k=1时,求得B、C的坐标,根据图象得到结论;
②分两种情况根据图象即可得到结论.
解:(1)直线x=3与直线y=![]() x+1交于点A,
x+1交于点A,
∴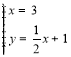 ,解得
,解得![]() ,
,
∴A(3,![]() );
);
(2)①当k=1时,根据题意B(3,![]() ),C(
),C(![]() ,
,![]() ),
),
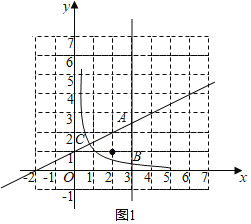
由图像可得,在W区域内有1个整数点:(2,1);
②若区域W内恰有1个整点,
当C点在直线x=3的左边时,如图1,在W区域内有1个整数点:(2,1),
∴1≤k<2;
当C点在直线x=3的右边时,如图2,在W区域内有1个整数点:(4,4),
∴16<k≤20;
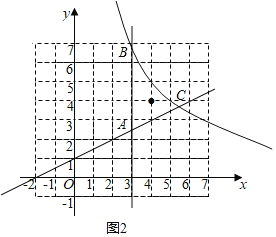
综上,当区域W内恰有1个整点时,1≤k<2或16<k≤20

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目