题目内容
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象经过点A(0,﹣4)和B(﹣2,2).
(1)求c的值,并用含a的式子表示b;
(2)当﹣2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;
(3)直线AB上有一点C(m,5),将点C向右平移4个单位长度,得到点D,若抛物线与线段CD只有一个公共点,求a的取值范围.
【答案】(1)b=2a﹣3;(2)![]() ≤a<0或0<a≤
≤a<0或0<a≤![]() ;(3)0<a<4或
;(3)0<a<4或![]() .
.
【解析】
(1)把点A(0,﹣4)和B(﹣2,2)分别代入y=ax2+bx+c,即可求解;
(2)当a<0时,依题意抛物线的对称轴需满足![]() ≤﹣2;当a>0时,依题意抛物线的对称轴需满足
≤﹣2;当a>0时,依题意抛物线的对称轴需满足![]() ≥0,即可求解;
≥0,即可求解;
(3)①当a>0时,若抛物线与线段CD只有一个公共点,则抛物线上的点(1,3a﹣7)在D点的下方,即可求解;②当a<0时,若抛物线的顶点在线段CD上,则抛物线与线段只有一个公共点,即可求解.
解:(1)把点A(0,﹣4)和B(﹣2,2)分别代入y=ax2+bx+c中,得
c=﹣4,4a﹣2b+c=2.
∴b=2a﹣3;
(2)当a<0时,依题意抛物线的对称轴需满足![]() ≤﹣2,
≤﹣2,
解得![]() ≤a<0.
≤a<0.
当a>0时,依题意抛物线的对称轴需满足![]() ≥0,
≥0,
解得 0<a≤![]() .
.
∴a的取值范围是![]() ≤a<0或0<a≤
≤a<0或0<a≤![]() ;
;
(3)设直线AB的表达式为:y=mx+n,则![]() ,解得:
,解得:![]() ,
,
故直线AB表达式为y=﹣3x﹣4,把C(m,5)代入得m=﹣3.
∴C(﹣3,5),由平移得D(1,5).
①当a>0时,若抛物线与线段CD只有一个公共点(如图1),
y=ax2+bx+c=ax2+(2a﹣3)﹣4,当x=1时,y=3a﹣7,
则抛物线上的点(1,3a﹣7)在D点的下方,
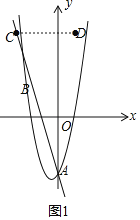
∴a+2a﹣3﹣4<5.
解得a<4.
∴0<a<4;
②当a<0时,若抛物线的顶点在线段CD上,
则抛物线与线段只有一个公共点(如图2),
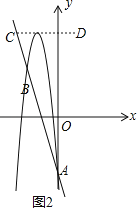
∴![]() .
.
即![]() .
.
解得![]() (舍去)或
(舍去)或![]() .
.
综上,a的取值范围是0<a<4或![]() .
.

【题目】为提升英语听力及口语技能,小明打算在手机上安装一款英语口语APP辅助练习.他分别从甲、乙、丙三款口语APP中随机选取了1000条网络评价进行对比,统计如下:
等级 评价数量 APP | 五星 | 四星 | 三星 | 二星 | 一星 | 合计 |
甲 | 562 | 286 | 79 | 48 | 25 | 1000 |
乙 | 517 | 393 | 52 | 21 | 17 | 1000 |
丙 | 504 | 210 | 136 | 116 | 34 | 1000 |
(说明:网上对于口语APP的综合评价从高到低依次为五星、四星、三星、二星和一星).
小明选择________(填“甲”、“乙”或“丙”)款英语口语APP,能获得良好口语辅助练习(即评价不低于四星)的可能性最大.