题目内容
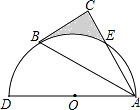
【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
(1)求AO的长;
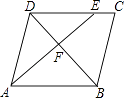
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC= ![]() AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答
【答案】
(1)
解:∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD= ![]() BD,
BD,
∵BD=24,
∴OB=12,
在Rt△OAB中,
∵AB=13,
∴OA= ![]() =
= ![]() =5.
=5.
(2)
证明:如图2,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴FA=FC,∠FAC=∠FCA,
由已知AF=AM,∠MAF=60°,
∴△AFM为等边三角形,
∴∠M=∠AFM=60°,
∵点M,F,C三点在同一条直线上,
∴∠FAC+∠FCA=∠AFM=60°,
∴∠FAC=∠FCA=30°,
∴∠MAC=∠MAF+∠FAC=60°+30°=90°,
在Rt△ACM中,∠ACM=180°﹣90°﹣60°=30°.
∴AC= ![]() AM.
AM.
(3)
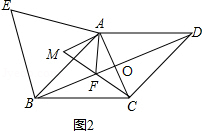
解:如图3,连接EM,
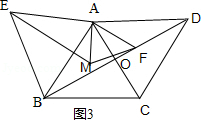
∵△ABE是等边三角形,
∴AE=AB,∠EAB=60°,
由(1)知△AFM为等边三角形,
∴AM=AF,∠MAF=60°,
∴∠EAM=∠BAF,
在△AEM和△ABF中,
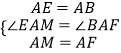 ,
,
∴△AEM≌△ABF(SAS),
∵△AEM的面积为40,△ABF的高为AO
∴ ![]() BFAO=40,BF=16,
BFAO=40,BF=16,
∴FO=BF﹣BO=16﹣12=4,
AF= ![]() =
= ![]() ,
,
∴△AFM的周长为3 ![]() .
.
【解析】(1)在Rt△OAB中,利用勾股定理OA= ![]() 求解.(2)由四边形ABCD是菱形,求出△AFM为等边三角形,∠M=∠AFM=60°,再求出∠MAC=90°,可得∠ACM=30°,即可.(3)求出△AEM≌△ABF,利用△AEM的面积为40求出BF,在利用勾股定理AF=
求解.(2)由四边形ABCD是菱形,求出△AFM为等边三角形,∠M=∠AFM=60°,再求出∠MAC=90°,可得∠ACM=30°,即可.(3)求出△AEM≌△ABF,利用△AEM的面积为40求出BF,在利用勾股定理AF= ![]() =
= ![]() =
= ![]() ,得出△AFM的周长为3
,得出△AFM的周长为3 ![]() .
.
【考点精析】通过灵活运用全等三角形的性质,掌握全等三角形的对应边相等; 全等三角形的对应角相等即可以解答此题.

【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?

【题目】铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次,记录如下:
学生 | 8次测试成绩(分) | 平均数 | 中位数 | 方差 | |||||||
甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 | 85 | 35.5 | |
乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 | 84 | ||
(1)请你在表中填上甲、乙两名学生这8次测试成绩的平均数、中位数和方差。(其中平均数和方差的计算要有过程).
(2)现要从中选派一人参加操作技能大赛,从统计学的角度考虑,你认为选派哪名同学参加合适,请说明理由.