题目内容
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y= ![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).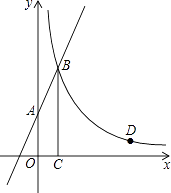
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y= ![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵BC⊥x轴于点C,且C点的坐标为(1,0),
∴在直线y=2x+3中,当x=1时,y=2+3=5,
∴点B的坐标为(1,5),
又∵点B(1,5)在反比例函数y= ![]() 上,
上,
∴k=1×5=5,
∴反比例函数的解析式为:y= ![]() ;
;
(2)解:将点D(a,1)代入y= ![]() ,得:a=5,
,得:a=5,
∴点D坐标为(5,1)
设点D(5,1)关于x轴的对称点为D′(5,﹣1),
过点B(1,5)、点D′(5,﹣1)的直线解析式为:y=kx+b,
可得: ![]() ,
,
解得: 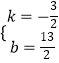 ,
,
∴直线BD′的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
根据题意知,直线BD′与x轴的交点即为所求点P,
当y=0时,得:﹣ ![]() x+
x+ ![]() =0,解得:x=
=0,解得:x= ![]() ,
,
故点P的坐标为( ![]() ,0).
,0).
【解析】(1)依据题意可得到点B的横坐标,然后可将点B的横坐标代入直线解析式可得到点B的纵坐标,最后,将点B的坐标代入反例函数的解析式求解即可;
(2)将y=1代入反比例函数解析式可求出点D的坐标,作点D关于x的轴的对称点D′,连接BD′,直线BD′与x轴的交点即为所求点P.

【题目】某农户以1500元/亩的单价承包了15亩地种植板栗,每亩种植80株优质板栗嫁接苗,购买嫁接苗,购买价格为5元/株,且每亩地的管理费用为800元,一年下来喜获丰收平均每亩板栗产量为600kg,已知当地板栗的批发和;零售价格分别如下表所示:
销售方式 | 批发 | 零售 |
售价(元/kg) | 10 | 14 |
通过市场调研发现,批发与零售的总销量只能达到总产量的70%,其中零售量不高于总销售量的40%,经多方协调当地食品加工厂承诺以7元/kg的价格收购该农户余下的板栗,设板栗全部售出后的总利润为y元,其中零售x kg.
(1)求y与x之间的函数关系
(2)求该农户所收获的最大利润
(总利润=总销售额-总承包费用-购买板栗苗的费用-总管理费用)