题目内容
【题目】如图，在⊙O中，半径OA＝6 cm，C是OB的中点，∠AOB＝120°，求阴影部分的面积．
【答案】阴影部分的面积为
cm2.
【解析】
过点C作CD⊥AO，交AO的延长线于点D，在Rt△OCD中，求得CD 的长，即可求得△AOC的面积，再求得扇形AOB的面积，利用S阴影＝S扇形OAB－S△AOC即可求得阴影部分的面积.
过点C作CD⊥AO，交AO的延长线于点D，
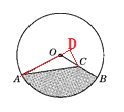
∵OB＝6 cm，C为OB的中点，∴OC＝3 cm.
∵∠AOB＝120°，∴∠COD＝60°.∴∠OCD＝30°.
∴在Rt△CDO中，OD＝
OC＝
cm.
∴CD＝
＝
＝
(cm)．
∴S△AOC＝AO·CD＝×6×＝
(cm2)．
又∵S扇形OAB＝
＝12π(cm2)，
∴S阴影＝S扇形OAB－S△AOC＝12π－＝
(cm2)，
即阴影部分的面积为cm2.
练习册系列答案
相关题目
