题目内容
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ![]() ,求AQ的长.
,求AQ的长.
【答案】
(1)
解:原命题不成立,新结论为:∠APB=90°,AF+BE=2AB(或AF=BE=AB),
理由:∵AM∥BN,
∴∠MAB+∠NBA=180°,
∵AE,BF分别平分∠MAB,NBA,
∴∠EAB= ![]() ∠MAB,∠FBA=
∠MAB,∠FBA= ![]() ∠NBA,
∠NBA,
∴∠EAB+∠FBA= ![]() (∠MAB+∠NBA)=90°,
(∠MAB+∠NBA)=90°,
∴∠APB=90°,
∵AE平分∠MAB,
∴∠MAE=∠BAE,
∵AM∥BN,
∴∠MAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,
同理:AF=AB,
∴AF=+BE=2AB(或AF=BE=AB);
(2)
解:如图1,
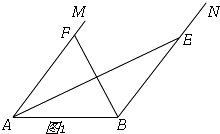
过点F作FG⊥AB于G,
∵AF=BE,AF∥BE,
∴四边形ABEF是平行四边形,
∵AF+BE=16,
∴AB=AF=BE=8,
∵32 ![]() =8×FG,
=8×FG,
∴FG=4 ![]() ,
,
在Rt△FAG中,AF=8,
∴∠FAG=60°,
当点G在线段AB上时,∠FAB=60°,
当点G在线段BA延长线时,∠FAB=120°,
①如图2,
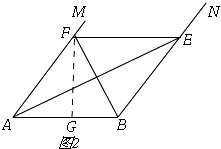
当∠FAB=60°时,∠PAB=30°,
∴PB=4,PA=4 ![]() ,
,
∵BQ=5,∠BPA=90°,
∴PQ=3,
∴AQ=4 ![]() ﹣3或AQ=4
﹣3或AQ=4 ![]() +3.
+3.
②如图3,
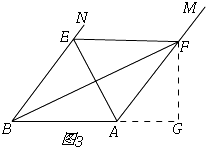
当∠FAB=120°时,∠PAB=60°,∠FBG=30°,
∴PB=4 ![]() ,
,
∵PB=4 ![]() >5,
>5,
∴线段AE上不存在符合条件的点Q,
∴当∠FAB=60°时,AQ=4 ![]() ﹣3或4
﹣3或4 ![]() +3.
+3.
【解析】(1)由角平分线和平行线整体求出∠MAB+∠NBA,从而得到∠APB=90°,最后用等边对等角,即可.(2)先根据条件求出AF,FG,求出∠FAG=60°,最后分两种情况讨论计算.此题是四边形综合题,主要考查了平行线的性质,角平分线的性质,直角三角形的性质,勾股定理,解本题的关键是用勾股定理计算线段.

 阅读快车系列答案
阅读快车系列答案