Question

【题目】如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和△BC′F的周长之和为（ ）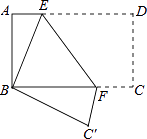
A.3
B.4
C.6
D.8

Answer 1

【答案】C
【解析】解：将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF， 由折叠特性可得，CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，
∵∠ABE+∠EBF=∠C′BF+∠EBF=90°
∴∠ABE=∠C′BF
在△BAE和△BC′F中，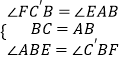
，
∴△BAE≌△BC′F（ASA），
∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3，
△ABE和△BC′F的周长=2△ABE的周长=2×3=6．
由折叠特性可得CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，推出∠ABE=∠C′BF，所以△BAE≌△BC′F，根据△ABE和△BC′F的周长=2△ABE的周长求解．