题目内容
【题目】平面直角坐标系中,A(m,n+2),B(m+4,n).
(1)当m=2,n=2时,
①如图1,连接AO、BO,求三角形ABO的面积;
②如图2,在y轴上是否存在点P,使三角形PAB的面积等于8,若存在,求P点坐标;若不存在,请说明理由;
(2)如图3,过A、B两点作直线AB,当直线AB过y轴上点Q(0,3)时,试求出m,n的关系式.
(温情提示:(a+b)×(c+d)=ac+ad+bc+bd)

【答案】(1)① 10;② 存在,P(0,9)或(0,1);(2)![]() .
.
【解析】
(1)①求出A、B两点坐标,利用分割法求出三角形的面积即可;②设P(0,m).直线AB的解析式为![]() ,设直线AB交y轴于C(0,5),由题意:
,设直线AB交y轴于C(0,5),由题意:![]() ,由此构建方程即可解决问题;
,由此构建方程即可解决问题;
(2)设直线AB的解析式为y=kx+b,则有: ,求出直线AB的解析式后利用待定系数法即可解决问题;
,求出直线AB的解析式后利用待定系数法即可解决问题;
解:(1)①当m=2,n=2时,A(2,4),B(6,2),
如图,过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 过
过![]() 轴于
轴于![]() ,过
,过![]() 过
过![]() 轴于
轴于![]()

∴![]()
②设P(0,m).如图,
设直线![]() 为
为![]() ,
,
把A(2,4),B(6,2)代入得:
![]()
解得:

![]() 直线AB的解析式为
直线AB的解析式为![]()
![]() 直线AB交y轴于C(0,5),
直线AB交y轴于C(0,5),
由题意:![]() ,
,
∴![]()
解得m=9或1,
∴P(0,9)或(0,1);
(2)设直线AB的解析式为y=kx+b,则有: ,
,
解得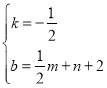 ,
,
∴直线AB的解析式为![]() ,
,
∵直线AB经过点Q(0,3),
∴![]() ,
,
∴![]() .
.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目






