题目内容
 (2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°.
(2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°.(1)求∠APB的大小;
(2)若PO=20cm,求△AOB的面积.
分析:(1)由PA、PB分别切⊙O于A、B,由切线的性质,即可得OA⊥PA,OB⊥PB,又由圆周角定理,求得∠AOB的度数,继而求得∠APB的大小;
(2)由切线长定理,可求得∠APO的度数,继而求得∠AOP的度数,易得PO是AB的垂直平分线,然后利用三角函数的性质,求得AD与OD的长,继而求得答案.
(2)由切线长定理,可求得∠APO的度数,继而求得∠AOP的度数,易得PO是AB的垂直平分线,然后利用三角函数的性质,求得AD与OD的长,继而求得答案.
解答:解:(1)∵PA、PB分别切⊙O于A、B,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∵∠C=60°,
∴∠AOB=2∠C=2×60°=120°,
∴∠APB=360°-∠PAO-∠PBO-∠AOB=60°;
(2)∵PA、PB分别切⊙O于A、B,
∴∠PAO=∠PBO=90°,∠APO=
∠APB=
×60°=30°,PA=PB,
∴P在AB的垂直平分线上,
∵OA=OB,
∴O在AB的垂直平分线上,
即OP是AB的垂直平分线,
即OD⊥AB,AD=BD=
AB,
∵∠PAO=90°,
∴∠AOP=60°,
在Rt△PAO中,AO=
PO=
×20=10(cm),
在Rt△AOD中,AD=AO•sin60°=10×
=5
(cm),OD=OA•cos60°=10×
=5(cm),
∴AB=2AD=10
cm,
∴△AOB的面积为:
AB•OD=
×10
×5=25
(cm2).
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∵∠C=60°,
∴∠AOB=2∠C=2×60°=120°,
∴∠APB=360°-∠PAO-∠PBO-∠AOB=60°;
(2)∵PA、PB分别切⊙O于A、B,
∴∠PAO=∠PBO=90°,∠APO=
| 1 |
| 2 |
| 1 |
| 2 |
∴P在AB的垂直平分线上,
∵OA=OB,
∴O在AB的垂直平分线上,
即OP是AB的垂直平分线,
即OD⊥AB,AD=BD=
| 1 |
| 2 |
∵∠PAO=90°,
∴∠AOP=60°,
在Rt△PAO中,AO=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOD中,AD=AO•sin60°=10×
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴AB=2AD=10
| 3 |
∴△AOB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了切线的性质、切线长定理、三角函数以及线段垂直平分线的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
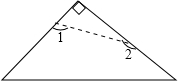 (2012•绵阳)如图,将等腰直角三角形虚线剪去顶角后,∠1+∠2=( )
(2012•绵阳)如图,将等腰直角三角形虚线剪去顶角后,∠1+∠2=( ) (2012•绵阳)如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )
(2012•绵阳)如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )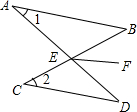 (2012•绵阳)如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=
(2012•绵阳)如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=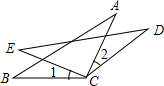 (2012•绵阳)如图,BC=EC,∠1=∠2,要使△ABC≌△DEC,则应添加的一个条件为
(2012•绵阳)如图,BC=EC,∠1=∠2,要使△ABC≌△DEC,则应添加的一个条件为 (2012•绵阳)如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积为
(2012•绵阳)如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积为