题目内容
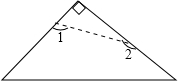（2012•绵阳）如图，将等腰直角三角形虚线剪去顶角后，∠1+∠2=（ ）分析：先根据等腰直角三角形的性质求出两底角的度数，再根据四边形内角和定理解答即可．
解答：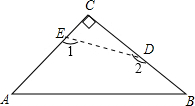
解：∵△ABC是等腰直角三角形，
∴∠A+∠B=90°，
∵四边形的内角和是360°，
∴∠1+∠2=360°-（∠A+∠B）=360°-90°=270°．
故选C．
解：∵△ABC是等腰直角三角形，∴∠A+∠B=90°，
∵四边形的内角和是360°，
∴∠1+∠2=360°-（∠A+∠B）=360°-90°=270°．
故选C．
点评：本题考查的是等腰直角三角形的性质及四边形内角和定理，熟知任意四边形的内角和是360°是解答此题的关键．
练习册系列答案
相关题目
（2012•绵阳）如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，已知∠AP′B=135°，P′A：P′C=1：3，则P′A：PB=（ ）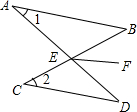
（2012•绵阳）如图，AB∥CD，AD与BC交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=
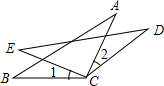（2012•绵阳）如图，BC=EC，∠1=∠2，要使△ABC≌△DEC，则应添加的一个条件为
（2012•绵阳）如图，正方形的边长为2，以各边为直径在正方形内画半圆，则图中阴影部分的面积为