题目内容
【题目】在△ABC中,∠ACB=90°,D是AB的中点,过点B作∠CBE=∠A,BE与射线CA相交于点E,与射线CD相交于点F.
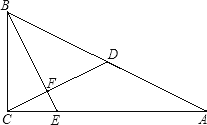
(1)如图,当点E在线段CA上时,求证:BE⊥CD;
(2)若BE=CD,那么线段AC与BC之间具有怎样的数量关系?并证明你所得到的结论;
(3)若△BDF是等腰三角形,求∠A的度数.
【答案】(1)证明见解析;(2)AC=2BC;(3)22.5°或67.5°.
【解析】
(1)根据角之间的等量关系及中点的特点即可得出答案;
(2)根据题意易证△BCE∽△ACB,根据相似三角形比例关系即可得出结论;
(3)分①点E在线段CA上时;②点E在线段CA延长线上讨论求解.
(1)∵∠ACB=90°,D是AB的中点,∴CD=AD,∴∠A=∠DCA.
∵∠CBE=∠A,∴∠DCA=∠CBE.
∵∠CBE+∠BEC=90°,∴∠BEC+∠DCA =90°,∴BE⊥CD;
(2)线段AC与BC之间的数量关系是:AC=2BC.
∵∠CBE=∠A,∠BCE=∠ACB,∴△BCE∽△ACB,∴![]() .
.
∵BE=CD,![]() ,∴
,∴![]() ,∴AC=2BC.
,∴AC=2BC.
(3)∵△BDF是等腰三角形,∠BFD=90°,∴∠BDF=45°.
①当点E在线段CA上时,如图1,∠A![]() ∠BDF=22.5°;
∠BDF=22.5°;
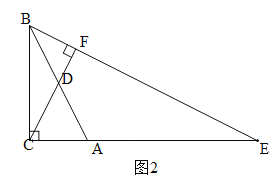
②当点E在线段CA延长线上时,如图2,∠CDA=∠BDF=45°,∠BAC![]() .
.
综上所述:∠BAC的度数为22.5°或67.5°.

练习册系列答案
相关题目