题目内容
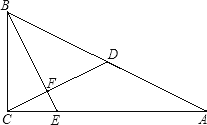
【题目】(1)问题发现:如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD与CF的数量关系是 ;BD与CF位置关系是 .
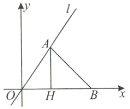
(2)拓展探究:如图2,当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
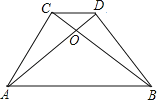
(3)解决问题:如图3,当△ABC绕点A逆时针旋转45°时,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,则线段DH的长为 .
时,则线段DH的长为 .

【答案】(1)BD=CF,BD⊥CF;(2)BD=CF成立,理由详见解析;(3)①详见解析;②DH=![]() .
.
【解析】
(1)易知,BD=CF,BD⊥CF;(2)先用“SAS”证明△CAF≌△BAD,再用全等三角形的性质即可得BD=CF成立;(3)利用△HFN与△AND的内角和以及它们的等角,得到∠NHF=90°,即可得①的结论;连接DF,延长AB,与DF交于点M,利用△BMD∽△FHD求解.
(1)易知,BD=CF,BD⊥CF,
故答案为:BD=CF,BD⊥CF;
(2)如图2中,BD=CF成立.

理由:由旋转得:AC=AB,∠CAF=∠BAD=θ;AF=AD,
在△ABD和△ACF中, ,
,
∴△ABD≌△ACF,
∴BD=CF.
(3)①证明:如图3中,

由(1)得,△ABD≌△ACF,
∴∠HFN=∠ADN,
∵∠HNF=∠AND,∠AND+∠AND=90°
∴∠HFN+∠HNF=90°
∴∠NHF=90°,
∴HD⊥HF,即BD⊥CF.
②如图4中,连接DF,延长AB,与DF交于点M.
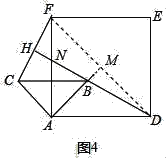
∵四边形ADEF是正方形,
∴∠MDA=45°,
∵∠MAD=45°
∴∠MAD=∠MDA,∠AMD=90°,
∴AM=DM,
∵AD=3![]() ,
,
在△MAD中,AM2+DM2=AD2,
∴AM=DM=3,
∴MB=AM﹣AB=3﹣2=1,
在Rt△BMD中,BM2+DM2=BD2,
∴BD=![]() =
=![]() .
.
在Rt△ADF中,AD=3![]() ,
,
∴DF=![]() AD=6,
AD=6,
由②知,HD⊥HF,
∴∠DHF=∠DMB=90°,
∵∠BDM=∠FDH,
∴△BDM∽△FDH,
∴![]() ,
,
∴DH=![]() =
=![]() .
.