题目内容
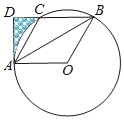
【题目】如图,⊙O的半径为6,点A,B,C为⊙O上三点,BA平分∠OBC,过点A作AD⊥BC交BC延长线于点D.
(1)求证:AD是⊙O的切线;
(2)当sin∠OBC=![]() 时,求BC的长;
时,求BC的长;
(3)连结AC,当AC∥OB时,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据切线的判定证明即可;
(2)过O点作OE⊥BC于点E,利用勾股定理和三角函数解答;
(3)连结OC,利用菱形的性质和直角三角形的性质解答即可.
(1)∵BA平分∠OBC,∴∠OBA=∠CBA.
∵OA=OB,∴∠OBA=∠OAB,∴∠OAB=∠CBA,∴AO∥BC.
∵AD⊥BC,∴AD⊥AO,∴直线AD是⊙O切线;
(2)过O点作OE⊥BC于点E,得BC=2BE.在Rt△OBE中,∵sin∠OBC=![]() ,∴
,∴![]() ,OB=6,∴OE=4,∴BE=
,OB=6,∴OE=4,∴BE=![]() ,∴
,∴![]() ;
;
(3)连结OC.
∵AO∥BC,AC∥OB,OA=OB,∴四边形OACB是菱形,∴OA=AC=OC=6,∴∠AOC=∠OAC=60°,∴∠DAC=30°,∴在Rt△ADC中,CD=6sin30°=3,∴AD=![]() ,∴
,∴![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.