��Ŀ����
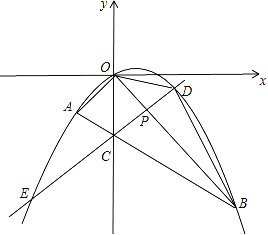
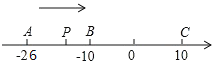
����Ŀ����֪��������A��B��C���㣬�ֱ��ʾ��������26����10��10������P��A��������ÿ��1����λ���ٶ������ƶ�����P���˶���C��ʱ�˶�ֹͣ������P�ƶ�ʱ��Ϊt����
(1)�ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺PA=_____��PC=_____��
(2)����P�˶���B��ʱ����Q��A��������ÿ��3����λ���ٶ������˶�����t���ڶ�����ʱP��Q��������?t���ڶ�����ʱP��Q�������4����λ����?
���𰸡�(1) t��36-t��(2)t=24��ʱ��P��Q����������t=22���26��ʱP��Q�������4����λ����.
��������
��1����������֮��ľ��룬�ɵ�P��A�͵�C�ľ��룻
��2���ٸ���·�̲�����з��̼�����⣬�ڸ��ݵ�P��Q���˶��ٶ���ʱ�����������Ҫ���ǵ�Q�ڵ�P����ߺ��ұ��������.
�⣺(1)PA=t��PC=36-t��
(2)�ٵ���P�˶���B��ʱ���˶��ľ���Ϊ��10-��-26��=16�������˶���ʱ��Ϊ16�룬����Q���˶�ʱ��Ϊ��t-16����P��Q��������ʱ���з��̣�3��t-16��=t,���t=24����
t����24��ʱP��Q����������
���ɢٿ�֪Q���˶�ʱ��Ϊ��t-16����
����Q�ڵ�P�����ʱ����ʱPQ=AP-AQ����4=t-3(t-16)�����t=22�룻
����Q�ڵ�P���ұ�ʱ����ʱPQ=AQ-AP����4=3(t-16)-t�����t=26��.
����t=22���26��ʱP��Q�������4����λ����.

 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�����Ŀ��ij������Ʊ�۸����±���ʾ��
��Ʊ���� | 1��50�� | 51��100�� | 100������ |
ÿ����Ʊ�� | 20Ԫ | 17Ԫ | 14Ԫ |
ijУ��һ��1����2��������ȥ�����������У�1�����������٣�����50�ˣ���2���������϶࣬����50�ˣ����Dz�����100�ˣ�����������Ϊ��λ�ֱ�Ʊ����һ��Ӧ��1912Ԫ�����������������������Ϊ�����幺Ʊ����ֻ�踶1456Ԫ
��1���з��̻��������������ж���ѧ����
��2������1����ȫԱ�μӣ���2������20�˲��μӴ˴λ���������һ����ʡǮ��ʽ����������Ʊ����˵�����ɣ�
��3������Ϊ�Ƿ���������Ŀ��ܣ�51��100��֮����Ʊ��Ǯ����100��������Ʊ��Ǯ����ȣ�����У��Ƕ��������������ƱǮ����ȣ���ֱ��д�����