Question

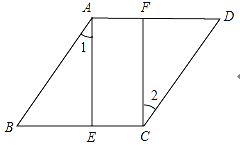
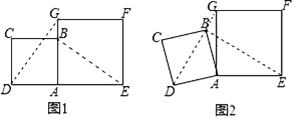
【题目】在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．

(1)小明发现DG=BE且DG⊥BE，请你给出证明．

(2)如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时△ADG的面积．

Answer 1

【答案】(1)证明见解析；(2)S△ADG=1+.

【解析】

（1）利用正方形得到条件，判断出△ADG≌△ABE，根据全等三角形的性质即可得到结论；
（2）利用正方形的性质在Rt△AMD中，∠MDA=45°，AD=2从而得出AM=DM=，在Rt△AMG中，AM2+GM2=AG2从而得出GM=即可．

(1)解：如图1，延长EB交DG于点H，

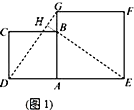
∵四边形ABCD与四边形AEFG是正方形，

∴AD=AB，∠DAG=∠BAE=90°，AG=AE

在△ADG与△ABE中，

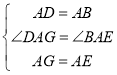
∴△ADG≌△ABE(SAS)，

∴∠AGD=∠AEB，

∵△ADG中∠AGD+∠ADG=90°，

∴∠AEB+∠ADG=90°，

∵△DEH中，∠AEB+∠ADG+∠DHE=180°，

∴∠DHE=90°，

∴DG⊥BE.

(2)解：如图2，过点A作AM⊥DG交DG于点M，

∠AMD=∠AMG=90°，

∵BD是正方形ABCD的对角，

∴∠MDA=45°

在Rt△AMD中，∵∠MDA=45°，AD=2，

∴AM=DM=，

在Rt△AMG中，

∵AM2+GM2=AG2，

∴GM=，

∵DG=DM+GM=，

∴S△ADG==1+.