题目内容
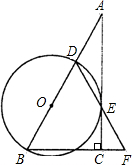
如图1,AB是⊙O的直径,射线BM⊥AB,垂足为B,点C为射线BM上的一个动点(C与B不重合),连接AC交⊙O于D,过点D作⊙O的切线交BC于E.
(1)在C点运动过程中,当DE∥AB时(如图2),求∠ACB的度数;
(2)在C点运动过程中,试比较线段CE与BE的大小,并说明理由;
(3)∠ACB在什么范围内变化时,线段DC上存在点G,满足条件BC2=4DG•DC(请写出推理过程).
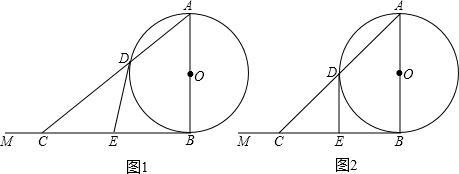
(1)在C点运动过程中,当DE∥AB时(如图2),求∠ACB的度数;
(2)在C点运动过程中,试比较线段CE与BE的大小,并说明理由;
(3)∠ACB在什么范围内变化时,线段DC上存在点G,满足条件BC2=4DG•DC(请写出推理过程).

(1)如图2:当DE∥AB时,连接OD,
∵DE是⊙O的切线,
∴OD⊥DE,
∵DE∥AB,
∴OD⊥AB;
又∵OD=OA,
∴∠A=45°,
又∵BM⊥AB,
∴∠OBE=90°,
∴在Rt△ABC中,∠ACB=45°;
即:当∠ACB=45°时,DE∥AB;
(本问证明的方法比较多,对于其它方法,只要是正确的,请参照给分)
(2)如图1,连接BD,
∵AB是⊙O的直径,
∴∠BDA=∠BDC=90°,
∴∠ACB+∠CBD=90°,
∠EDB+∠CDE=90°;
又∵BM⊥AB,AB是⊙O的直径,
∴MB是⊙O的切线,
又∵DE是⊙O的切线,
∴∠CBD=∠EDB,
∴∠ACB=∠CDE,
∴EC=ED,
∴BE=EC;
(3)假设在线段CD上存在点G,使BC2=4DG•DC,
由(2)知:BE=CE,
∴BC=2CE=2DE,
∴(2DE)2=4 DG•DC,从而DE2=DG•DC;
由于∠CDE是公共角,
∴△DEG∽△DCE,
∴∠ACB=∠DEG;
令∠ACB=x,∠DGE=y,
∴∠CDE=∠ACB=x,
∵C和B不重合,
∴BC>0,
∴D和G就不能够重合,但是,G可以和C重合,
∴要使线段CD上的G点存在,则要满足:2x+y=180°且y≥x,因此x≤60°,
∴0°<∠ACB≤60°时,满足条件的G点存在.


练习册系列答案
相关题目