题目内容
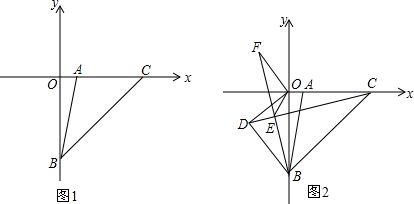
如图,在直角坐标系xOy中,直线AB交x轴于A(1,0),交y轴负半轴于B(0,-5),C为x轴正半轴上一点,且CA=
CO.
(1)求△ABC的面积.
(2)延长BA到P,使得PA=AB,求P点的坐标.
(3)如图,D是第三象限内一动点,且OD⊥BD,直线BE⊥CD于E,OF⊥OD交BE延长线于F.当D点运动时,
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
| 4 |
| 5 |
(1)求△ABC的面积.
(2)延长BA到P,使得PA=AB,求P点的坐标.
(3)如图,D是第三象限内一动点,且OD⊥BD,直线BE⊥CD于E,OF⊥OD交BE延长线于F.当D点运动时,
| OD |
| OF |

分析:(1)由A和B的坐标可求出AC的长,再根据三角形的面积公式即可求出△ABC的面积;
(2)作PN⊥x轴于N,通过证明△PAN≌△BAO,可求出PN和ON的长,即可得到P点的坐标;
(3)当D点运动时,
的大小不发生变化,设BF与OD的交点为M,利用已知条件证明△FOB≌△DOC,得到OF=OD,求出OD:OF=1.
(2)作PN⊥x轴于N,通过证明△PAN≌△BAO,可求出PN和ON的长,即可得到P点的坐标;
(3)当D点运动时,
| OD |
| OF |
解答:解:(1)∵点A(1,0),点B(0,-5),
∴OA=1,OB=5,
∵CA=
CO,
∴CA=4,CO=5,
∴S△ABC=
AC•OB=
×4×5=10;
(2)作PN⊥x轴于N,
在△PAN和△BAO中,
,
∴△PAN≌△BAO(AAS),
∴PN=OB,AN=AO,
∴PN=5,ON=2OA=2,
∴P(2,5);
(3)当D点运动时,
的大小不发生变化,
理由如下:
设BF与OD的交点为M,
∵OF⊥OD,
∴∠F+∠∠FMD=90°,
又∵BE⊥CD,
∴∠FMD+∠DME=90°,
∵∠FMD=∠DME,
∴∠F=∠MDE,
∵OF⊥OD,OB⊥OC,
∴∠FOD=∠COB=90°,
∴∠FOD+∠DOB=∠COB+∠DOB,
∴∠FOB=∠DOC,
在△FOB和△DOC中,
,
∴△FOB≌△DOC(AAS),
∴OF=OD,
∴
=1.
∴OA=1,OB=5,
∵CA=
| 4 |
| 5 |

∴CA=4,CO=5,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)作PN⊥x轴于N,
在△PAN和△BAO中,
|
∴△PAN≌△BAO(AAS),
∴PN=OB,AN=AO,
∴PN=5,ON=2OA=2,
∴P(2,5);
(3)当D点运动时,
| OD |
| OF |
理由如下:
设BF与OD的交点为M,
∵OF⊥OD,
∴∠F+∠∠FMD=90°,
又∵BE⊥CD,
∴∠FMD+∠DME=90°,
∵∠FMD=∠DME,
∴∠F=∠MDE,
∵OF⊥OD,OB⊥OC,
∴∠FOD=∠COB=90°,
∴∠FOD+∠DOB=∠COB+∠DOB,
∴∠FOB=∠DOC,
在△FOB和△DOC中,
|
∴△FOB≌△DOC(AAS),
∴OF=OD,
∴
| OD |
| OF |
点评:本题考查了三角形的面积公式以及全等三角形的判定与性质等知识点,题目的综合性很强,难度不小.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N. 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.