题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(1)求![]() 的大小;
的大小;
(2)求证:![]() .
.

【答案】(1)∠CAD =22.5°;(2)见解析.
【解析】
(1)只要证明△BDF≌△ADC,推出BD=AD,推出∠BAD=∠ABD=45°=2∠CBE=2∠DAC即可解决问题.
(2)延长BE、DG交于点K.证明DK=BD=AD, GK=AF后可以证明Rt△AEF≌Rt△KEG,问题即可解决.
证明:(1)∵AD⊥BC,
∴∠ADC=90°
∵AB=BC,E为AC中点,
∴∠ABE=∠CBE= ![]() ∠ABC,BE⊥AC,
∠ABC,BE⊥AC,
∴∠BEC=90°,
∴180°-∠C-∠ADC=180°-∠C-∠BEC
即∠CBE=∠CAD,
在△BDF和△ADC中,
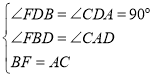 ,
,
∴△BDF≌△ADC,
∴BD=AD,
∴∠BAD=∠ABD=45°,∠CBE=∠DAC,
∴∠CAD=![]() ∠ABD=22.5°.
∠ABD=22.5°.
(2)延长BE、DG交于点K.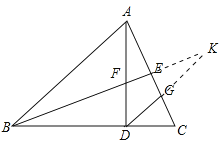
∵DG∥AB,
∴∠CGD=∠CAB,∠K=∠ABE,
∵∠BAC=∠C, ∠ABE=∠CBE=∠EAF
∴∠CGD=∠C,∠K=∠CBE =∠EAF
∴DG=DC,DK=BD,
∴△BDF≌△ADC,
∴CD=DF,
∴DG=DF,DK=BD=AD,
∴DK-DG=AD-DF,
即GK=AF
在Rt△AEF和Rt△KEG中
 ,
,
∴Rt△AEF≌Rt△KEG(AAS),
∴EF=EG.

练习册系列答案
相关题目





