Question

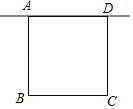
【题目】如图，在矩形ABCD中，AB=3，点P是直线AD上一点，若满足△PBC是等腰三角形的点P有且只有3个，则AD的长为______．

Answer 1

【答案】3或2

【解析】①如图，当AB=AD时

满足△PBC是等腰三角形的点P有且只有3个，

△P1BC,△P2BC是等腰直角三角形,△P3BC是等腰直角三角形(P3B=P3C)，

则AB=AD=3.

②当AB<AD，且满足△PBC是等腰三角形的点P有且只有3个时，如图，

易知P2是AD的中点,BC=BP1=BP2=CP2=CP3，

此时易知△P2BC是等边三角形，

在Rt△ABP2中,∵AB=3,∠ABP2=30°，

∴AP2=ABtan30°=，

∴BC=AD=2AP2=

③当AB>AD时，直线AD上只有一个点P满足△PBC是等腰三角形。

故答案为：3或.