��Ŀ����
����Ŀ��2016����ѧ�ڣ�����ijѧУ��չ���ԡ����Ρ��ж���Ϊ����İ�ӻ�������������2������ѧ��ȤС�������5����Ҫ�۵㲢�ڱ���ѧ���н����˵��飨Ҫ��ÿλͬѧֻѡ�Լ����Ͽɵ�һ��۵㣩�����Ƴ�������ͳ��ͼ���������ͳ��ͼ������������⣺
��1���ð��������ˣ�ѧ��ѡ��ȡ���۵���������ˣ�������ͳ��ͼ�У�����г���۵��������������Բ�Ľ��������ȣ�
��2�������У��500������ѧ����������������ѡ�ж����۵�ij���ѧ��Լ�������ˣ�
��3�������ѧ��ȤС������5����Ҫ�۵�����ѡ����۵���ȫУѧ���н��е��飬��ǡ��ѡ������г���͡��ж����۵�ĸ��ʣ�����״ͼ���б���������𣩣�
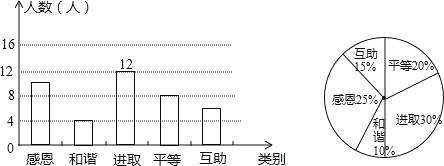
���𰸡���1���ð�������Ϊ40�ˣ�ѧ��ѡ��ȡ���۵������Ϊ12������г���۵��������������Բ�Ľ�Ϊ36�㣻
��2������ѡ�ж����۵�ij���ѧ��Լ��125�ˣ�
��3������״ͼ��������ǡ��ѡ������г���͡��ж����۵�ĸ���Ϊ![]() .
.
����������������1��������ͳ��ͼ�õ�ѧ��ѡ��ȡ���۵������Ϊ12��Ȼ����12��������ռ�İٷֱȵõ�ȫ������������360����ԡ���г���۵���ռ�İٷֱȵõ�����г���۵��������������Բ�Ľǣ���2����500���������С��ж����۵���ռ�İٷֱȿɹ��Ƴ�ѡ�ж����۵�ij���ѧ��������3������״ͼ��ƽ�ȡ���ȡ����г���ж�����������������Ǣ٢ڢۢܢݣ�չʾ����20�ֵȿ��ܵĽ���������ҳ�ѡ������г���͡��ж����۵�Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
�����������1���ð�������Ϊ12��30%=40���ˣ���ѧ��ѡ��ȡ���۵������Ϊ12��������ͳ��ͼ�У�����г���۵��������������Բ�Ľ�=360���10%=36�㣻
��2��500��25%=125��
���Թ���ѡ�ж����۵�ij���ѧ��Լ��125�ˣ�
�ʴ�Ϊ40��12��36��125��
��3������״ͼΪ������ƽ�ȡ���ȡ����г���ж�����������������Ǣ٢ڢۢܢݣ�
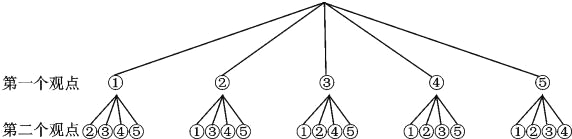
����20�ֵȿ��ܵĽ����������ѡ������г���͡��ж����۵�Ľ����Ϊ2��
����ǡ��ѡ������г���͡��ж����۵�ĸ���=![]() =
=![]() ��
��

 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�