题目内容
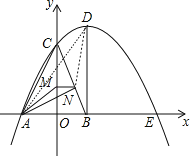
【题目】如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.

【答案】(1)抛物线解析式为y=﹣![]() x2+
x2+![]() x+4;D点坐标为(3,5);(2)M点的坐标为(0,
x+4;D点坐标为(3,5);(2)M点的坐标为(0,![]() )或(0,
)或(0,![]() );(3)AM+AN的最小值为
);(3)AM+AN的最小值为![]() .
.
【解析】(1)利用待定系数法求抛物线解析式;利用等腰三角形的性质得B(3,0),然后计算自变量为3所对应的二次函数值可得到D点坐标;
(2)利用勾股定理计算出BC=5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,由于∠MCN=∠OCB,根据相似三角形的判定方法,当![]() 时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即
时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即![]() ;当
;当![]() 时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即
时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即![]() ,然后分别求出m的值即可得到M点的坐标;
,然后分别求出m的值即可得到M点的坐标;
(3)连接DN,AD,如图,先证明△ACM≌△DBN,则AM=DN,所以AM+AN=DN+AN,利用三角形三边的关系得到DN+AN≥AD(当且仅当点A、N、D共线时取等号),然后计算出AD即可.
(1)把A(﹣3,0),C(0,4)代入y=ax2﹣5ax+c得![]() ,解得
,解得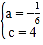 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
∵AC=BC,CO⊥AB,
∴OB=OA=3,
∴B(3,0),
∵BD⊥x轴交抛物线于点D,
∴D点的横坐标为3,
当x=3时,y=﹣![]() ×9+
×9+![]() ×3+4=5,
×3+4=5,
∴D点坐标为(3,5);
(2)在Rt△OBC中,BC=![]() =5,
=5,
设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,
∵∠MCN=∠OCB,
∴当![]() 时,△CMN∽△COB,则∠CMN=∠COB=90°,
时,△CMN∽△COB,则∠CMN=∠COB=90°,
即![]() ,解得m=
,解得m=![]() ,此时M点坐标为(0,
,此时M点坐标为(0,![]() );
);
当![]() 时,△CMN∽△CBO,则∠CNM=∠COB=90°,
时,△CMN∽△CBO,则∠CNM=∠COB=90°,
即![]() ,解得m=
,解得m=![]() ,此时M点坐标为(0,
,此时M点坐标为(0,![]() );
);
综上所述,M点的坐标为(0,![]() )或(0,
)或(0,![]() );
);
(3)连接DN,AD,如图,
∵AC=BC,CO⊥AB,
∴OC平分∠ACB,
∴∠ACO=∠BCO,
∵BD∥OC,
∴∠BCO=∠DBC,
∵DB=BC=AC=5,CM=BN,
∴△ACM≌△DBN,
∴AM=DN,
∴AM+AN=DN+AN,
而DN+AN≥AD(当且仅当点A、N、D共线时取等号),
∴DN+AN的最小值=![]() ,
,
∴AM+AN的最小值为![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案