题目内容
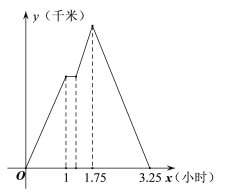
【题目】已知A地，火神山医院、B地顺次在一条笔直的公路上，且A地、B地距火神山医院的路程相同，甲、乙两家车队分别从A、B两地向火神山医院运送货物，甲车队比乙车队晚出发0.75小时． 为避免拥堵，总调度部门通知距火神山医院更近的车队进工地卸货（卸货时间忽略不计），然后原路原速返回，而另一车队则在火神山医院40千米处等待直到另一车队卸货完毕后再按原速继续行驶进入工地，卸货后原路原速返回． 甲车队距A地的路程
（千米）与甲车队行驶的时间
（小时）之间的函数关系如图所示：
（1）甲车队的速度为 千米/时，乙车队的速度为 千米/时，A地与火神山医院之间的距离为 千米．
（2）甲车队原路返回时与之间的函数关系式．
（3）直接写出两车队相距80千米时的值．
【答案】（1） 80，
，120；（2）
；（3）
，
.
【解析】
（1）文字信息与图象相结合，有甲车队距火神山医院40千米时，乙车队到达火神山医院卸货．甲车队卸货后返回A地用时1.5小时．据此列方程解答即可；
（2）运用待定系数法解答，即可求出关系式；
（3）根据题意可分为两种情况，在乙车队没有到达火神山医院前和在甲车队卸货结束后，分别列方程解答即可．
解：（1）设甲车队速度为
千米/时，
，
∴
，
∴
千米.
∴ 
千米/时.
故答案为：80，，120；
（2）设返回时一次函数为
.
有
，
解得：
，
，
∴ .
（3）在乙车队没有到达火神山医院前，有
，
解得：
；
在甲车队卸货结束后，有
，
解得：
；
∴两车队相距80千米时x的值为或.
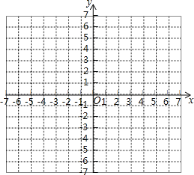
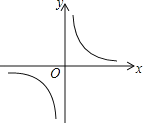
孟建平小学滚动测试系列答案
【题目】某班数学兴趣小组根据学习函数的经验，通过列表、描点、连线的方法对函数 y＝
的图象与性质进行了研究，研究过程如下，请补充完整．
（1）y 与 x 的几组对应值如下表：
x | … | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | … |
y | … |
|
| 6 | 6 | m |
| … |
函数 y＝的自变量 x 的取值范围是 ，m 的值为 ；
（2）在给出的平面直角坐标系中，描出以上表中各组对应值为坐标的点，画出函数 y＝的大致图象，并写出该函数的两条性质；
（3）在同一坐标系中画出函数 y1＝
x 的图象，并根据图象直接写出当 y＞y1 时，自变量 x 的取值范围．
