��Ŀ����
����Ŀ��һ��װ���������ijƷ��ͯװ��ÿ������120Ԫ��������200Ԫ�������Żݣ�����һ����10�����ϵģ�ÿ����һ���������ȫ����װÿ���ͽ���1Ԫ��������ͼ�ΪΪÿ��160Ԫ��
��1����һ����������ټ�����������ͼ۹���
��2��д����װ��һ������x��ʱ��������y��Ԫ����x������֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��һ�죬��������46������������50��������ȴ������46����Ǯ��������50����Ǯ�࣬��������ѧ֪ʶ������һ������Ϊ�˲��������������������Ż��������������£����Ӧ����ͼ�ÿ��160Ԫ������ߵ����٣�
���𰸡���1��һ��������50������������ͼ۹���2��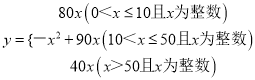 ����3�����Ӧ����ͼ�ÿ��160Ԫ������ߵ�165Ԫ��
����3�����Ӧ����ͼ�ÿ��160Ԫ������ߵ�165Ԫ��
�������������������1����һ��������x������ÿ���ļ۸�Ϊ[200-��x-10��]Ԫ�����ݽ��ۺ�ļ۸�Ϊ160Ԫ�������������⼴�ɣ�
��2������������=����������ÿ֧������������ʽ���ɣ�
��3�����ݣ�2���Ľ�����Ϊ����ʽ�����ݶ���ʽ�����ʾͿ���������ۣ�
���������
��1����һ��������x������������ͼ۹��������⣬��
200����x��10����1=160��
��ã�x��50��
��һ��������50������������ͼ۹���
��2����0��x��10ʱ��y��(200��120)x��80x
��10��x��50ʱ��y��[��200��120������x��10����1] ��x����x2+90x��
��x��50ʱ��y��(160��120)x��40x��
���ϣ�y��x�Ĺ�ϵʽΪ 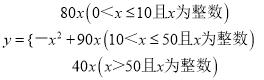
��3����y����x2+90x����(x��45)2+2025 ֪�Գ���x��45��
��45��x��50ʱ��y��x���������С���������ļ���Խ��ʱ������ԽС��
����������46����Ǯ����50���ӵ�Ǯ�������
��x��45ʱ������ۼ�Ϊ200����45��10����165��Ԫ����
��Ϊ�˲��������������������Ż��������������£����Ӧ����ͼ�ÿ��160Ԫ������ߵ�165Ԫ��