题目内容
如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点(点P不与点B、C重合).现将△PCD沿PD翻折,得到△PC’D;作∠BPC’的角平分线,交AB于点E.设BP=" x,BE=" y,则下列图象中,能表示y与x的函数关系的图象大致是( )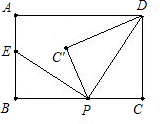
A、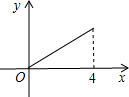 B、
B、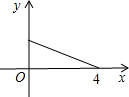 C、
C、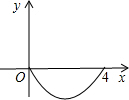 D、
D、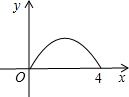
D.
解析试题分析:根据题意,连接DE,因为△PCD沿PD翻折,得到△PC′D,故有DP平分∠CPC′;又PE为∠BPC′的角平分线,可推知∠EPD=90°,又因为BP=x,BE=y,BC=4,AB=3,分别用x和y表示出PD和EP和DE,在Rt△PED中利用勾股定理,即可得出一个关于x和y的关系式,化简即可:
如图,连接DE,
∵△PCD沿PD翻折,得到△PC′D,∴DP平分∠CPC′.
又∵PE为∠BPC′的角平分线,∴∠EPD=90°.
∵BP=x,BE=y,BC=4,AB=3,
∴Rt△PCD中,PC=4-x,DC=3,故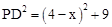 ,
,
在Rt△EBP中,BP=x,BE=y,故PE2=x2+y2,
在Rt△ADE中,AE=3-y,AD=4,故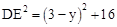 ,
,
在Rt△PDE中,DE2=PD2+PE2,即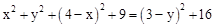 ,化简得:
,化简得: .
.
结合题意,它是开口向下的抛物线,只有选项D符合题意.
故选D.
考点:1.动点问题的函数图象;2.翻折问题;3.勾股定理;4.数形结合思想的应用.

抛物线y=2(x﹣3)2+1的顶点坐标是( )
| A.(3,1) | B.(3,﹣1) | C.(﹣3,1) | D.(﹣3,﹣1) |
如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系式中不正确的是( )
| A.h=m | B.n>h | C.k>n | D.h>0,k>0 |
将抛物线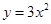 先向上平移3个单位,再向左平移2个单位后得到的抛物线解析式为( )
先向上平移3个单位,再向左平移2个单位后得到的抛物线解析式为( )
A. | B. |
C. | D. |
若x1,x2(x1<x2)是方程(x-a)(x-b)=1(a<b)的两个根,则实数x1,x2,a,b的大小关系为( )
| A.x1<x2<a<b | B.x1<a<x2<b | C.x1<a<b<x2 | D.a<x1<b<x2 |
下列函数有最大值的是 ( )
A. | B. | C. | D. |
若二次函数 的图象经过点P(-2,4),则该图象必经过点( )
的图象经过点P(-2,4),则该图象必经过点( )
| A.(2,4) | B.(-2,-4) | C.(-4,2) | D.(4,-2) |
 ,下列说法中错误的个数是( )
,下列说法中错误的个数是( ) 轴有交点,则
轴有交点,则 .
. 上,则
上,则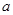 的值为
的值为 .
. 时,不等式
时,不等式 的解集是
的解集是 .
. ,则
,则 .
.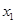 、
、 ,则当x取
,则当x取 时的函数值与x取0时的函数值相等.
时的函数值与x取0时的函数值相等.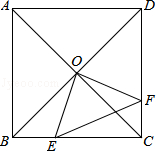
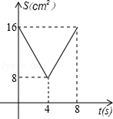 B.
B.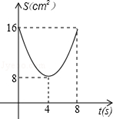 C.
C.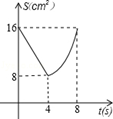 D,
D,