题目内容
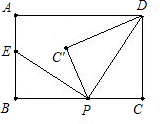
如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为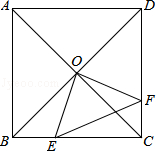
A.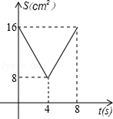 B.
B.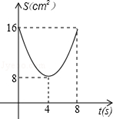 C.
C.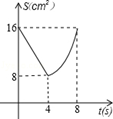 D,
D,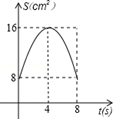
B
解析试题分析:根据题意BE=CF=t,CE=8﹣t,
∵四边形ABCD为正方形,∴OB=OC,∠OBC=∠OCD=45°。
∵在△OBE和△OCF中,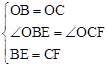 ,∴△OBE≌△OCF(SAS)。∴
,∴△OBE≌△OCF(SAS)。∴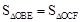 。
。
∴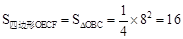 。
。
∴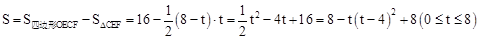 。
。
∴s(cm2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t≤8。
故选B。

练习册系列答案
相关题目
已知二次函数 ,则下列说法正确的是( )
,则下列说法正确的是( )
| A.y有最小值0,有最大值-3 |
| B.y有最小值-3,无最大值 |
| C.y有最小值-1,有最大值-3 |
| D.y有最小值-3,有最大值0 |
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
错误的个数有【 】
| A.1个 | B.2个 | C.3个 | D.4个 |
若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(﹣2,0),则抛物线y=ax2+bx的对称轴为【 】
| A.直线x=1 | B.直线x=﹣2 | C.直线x=﹣1 | D.直线x=﹣4 |
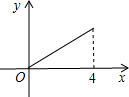 B、
B、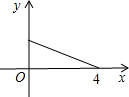 C、
C、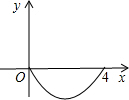 D、
D、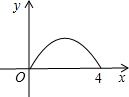
 ,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为
,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为 中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的
中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的



 的图象如图所示,则一次函数
的图象如图所示,则一次函数 与反比例函数
与反比例函数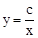 在同一平面直角坐标系中的大致图象为【 】
在同一平面直角坐标系中的大致图象为【 】



