��Ŀ����
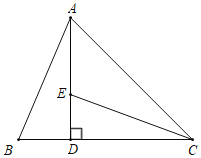
����Ŀ����ͼ���ڡ�ABC�У�AB��BC��AD��BC�ڵ�D��BE��AC�ڵ�E��AD��BE���ڵ�F��BH��AB�ڵ�B����M��BC���е㣬����FM���ӳ���BH�ڵ�H��
��1����ͼ���У���ABC��60�㣬AF��3ʱ��FC���� ����BH���� ����
��2����ͼ���У���ABC��45�㣬AF��2ʱ��FC���� ����BH���� ����
��3���ӵڣ�1������2�����㷢����ʲô���ɣ���ͼ���У���ABC��30�㣬AF��1ʱ���Բ���BH���ڶ��٣���֤����IJ��룮
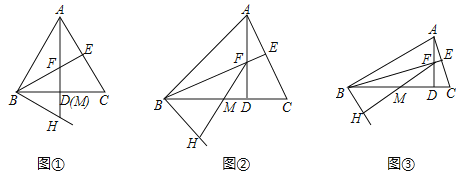
���𰸡���1��3��3����2��2��2����3���ӵڣ�1������2���з���AF��CF��BH�� BH��1��������
��������
��1����ͼ������CF���ɴ��ĵ����ʿɵ�CF��AB���ɵ�CF��BH���ɡ�ASA����֤��BMH�ա�CMF���ɵ�BH��CF�����߶δ�ֱƽ���ߵ����ʿɵ�AF��CF���ɵ�AF��CF��BH��3��
��2����ͼ������CF���ɴ��ĵ����ʿɵ�CF��AB���ɵ�CF��BH���ɡ�ASA����֤��BMH�ա�CMF���ɵ�BH��CF�����߶δ�ֱƽ���ߵ����ʿɵ�AF��CF���ɵ�AF��CF��BH��2��
��3����ͼ������CF���ɴ��ĵ����ʿɵ�CF��AB���ɵ�CF��BH���ɡ�ASA����֤��BMH�ա�CMF���ɵ�BH��CF�����߶δ�ֱƽ���ߵ����ʿɵ�AF��CF���ɵ�AF��CF��BH��1��
�⣺��1����ͼ������CF��
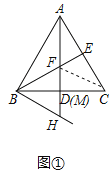
��AD��BC��BE��AC��
��CF��AB��
��BH��AB��
��CF��BH��
���CBH����BCF��
�ߵ�M��BC���е㣬
��BM��MC��
�ڡ�BMH�͡�CMF�У�
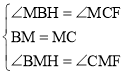 ��
��
���BMH�ա�CMF��ASA����
��BH��CF��
��AB��BC��BE��AC��
��BE��ֱƽ��AC��
��AF��CF��
��BH��AF��
��AF��CF��BH��3��
��2����ͼ�ڣ�����CF��
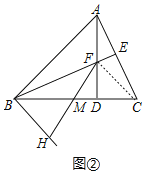
��AD��BC��BE��AC��
��CF��AB��
��BH��AB��
��CF��BH��
���CBH����BCF��
�ߵ�M��BC���е㣬
��BM��MC��
�ڡ�BMH�͡�CMF�У�
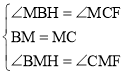
���BMH�ա�CMF��ASA����
��BH��CF��
��AB��BC��BE��AC��
��BE��ֱƽ��AC��
��AF��CF��
��BH��AF��
��AF��CF��BH��2��
��3���ӵڣ�1������2���з���AF��CF��BH��
����BH��1��
�������£�
��ͼ�ۣ�����CF��
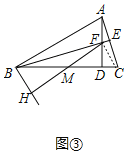
��AD��BC��BE��AC��
��CF��AB��
��BH��AB��
��CF��BH��
���CBH����BCF��
�ߵ�M��BC���е㣬
��BM��MC��
�ڡ�BMH�͡�CMF�У�
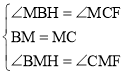
���BMH�ա�CMF��ASA����
��BH��CF��
��AB��BC��BE��AC��
��BE��ֱƽ��AC��
��AF��CF��
��BH��AF��
��AF��CF��BH��1��