Question

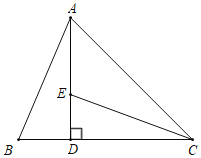
【题目】如图，在△ABC中，∠ACB＝45°，过点A作AD⊥BC于点D，点E为AD上一点，且ED＝BD．

（1）求证：△ABD≌△CED；

（2）若CE为∠ACD的角平分线，求∠BAC的度数．

Answer 1

【答案】（1）见解析；（2）∠BAC＝67.5°．

【解析】

（1）证出△ADC是等腰直角三角形，得出AD＝CD，∠CAD＝∠ACD＝45°，由SAS证明△ABD≌△CED即可；

（2）由角平分线定义得出∠ECD＝∠ACD＝22.5°，由全等三角形的性质得出∠BAD＝∠ECD＝22.5°，即可得出答案．

解：（1）证明：∵AD⊥BC，∠ACB＝45°，

∴∠ADB＝∠CDE＝90°，△ADC是等腰直角三角形，

∴AD＝CD，∠CAD＝∠ACD＝45°，

在△ABD与△CED中，，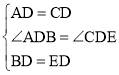

∴△ABD≌△CED（SAS）；

（2）解：∵CE为∠ACD的角平分线，

∴∠ECD＝∠ACD＝22.5°，

由（1）得：△ABD≌△CED，

∴∠BAD＝∠ECD＝22.5°，

∴∠BAC＝∠BAD+∠CAD＝22.5°+45°＝67.5°．