题目内容
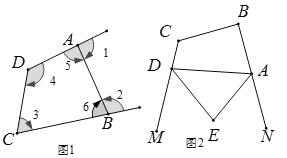
【题目】(1)如图1,试探究其中∠1,∠2与∠3,∠4之间的关系,并证明.
(2)用(1)中的结论解决下列问题:如图2,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
【答案】(1)∠1+∠2=∠3+∠4(2)60°
【解析】
(1)由四边形的内角和是360°,以及邻补角的和是180°求解即可;
(2)依据(1)的结论可知∠MDA+∠DAN=240°,由角平分线的定义可求得∠EDA+∠EAD=120°,最后在△ADE中由勾股定理可求得∠E的度数.
(1)∠1+∠2=∠3+∠4,理由如下:
由四边形的内角和是360°可知:∠3+∠4+∠5+∠6=360°,
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2+∠5+∠6=360°,
∴∠1+∠2=∠3+∠4;
(2)由(1)可知∠MDA+∠DAN=∠B+∠C=240°,
∵AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,
∴∠EDA=![]() ∠MDA,∠EAD=
∠MDA,∠EAD=![]() ∠DAN,
∠DAN,
∴∠EDA+∠EAD=![]() ×(∠MDA+∠DAN)=
×(∠MDA+∠DAN)=![]() ×240°=120°,
×240°=120°,
∴∠E=180°-(∠EDA+∠EAD) =180°-120°=60°.

练习册系列答案
相关题目