题目内容
【题目】阅读下列文字:
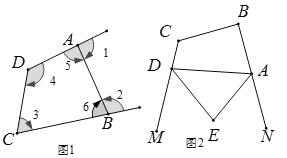
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
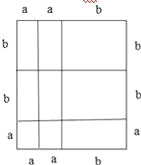
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,
①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.即2a2+5ab+2b2=______.

【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)a2+b2+c2=45;
(3)①画图见解析;②2a2+5ab+2b2=(2a+b)(a+2b).
【解析】试题分析:(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.(2)根据利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.(3)①找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件;②根据所给的规律分解因式即可.
试题解析:
(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,
=112﹣2×38=45;
(3)
①如图所示,
②如上图所示的矩形面积=(2a+b)(a+2b),
它是由2个边长为a的正方形、5个边长分别为a、b的长方形、2个边长为b的小正方形组成,所以面积为2a2+5ab+2b2,则2a2+5ab+2b2=(2a+b)(a+2b),
故答案为:2a2+5ab+2b2=(2a+b)(a+2b).