题目内容
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(3,0),与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<0),过点P作PD⊥BC于点D.
①求线段PD的长的最大值;②当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.
【答案】
(1)解:设抛物线所对应的函数关系式为y=ax2+bx+c
将A(﹣1,0),B(3,0),C(0,3)代入y=ax2+bx+c得  ,解得
,解得 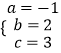
∴抛物线所对应的函数关系式为y=﹣x2+2x+3;
(2)解:①过P作PN⊥x轴于点N,交BC于点E,如图1,
设直线BC解析式为y=kx+b,
把B(3,0),C(0,3)代入y=kx+b得 ![]() ,解得:k=﹣1,b=3,
,解得:k=﹣1,b=3,
∴直线BC解析式为y=﹣x+3,
设点P的坐标为(t,﹣t2+2t+3),则E(t,﹣t+3),
∴PE=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,
∵OB=OC=3,
∴∠OBC=45°
∵PD⊥BC,
∴∠PED=45°,
∴△PDE为等腰直角三角形,
∴PD= ![]() PE=
PE= ![]() (﹣t2+3t)=﹣
(﹣t2+3t)=﹣ ![]() ,
,
∴当t= ![]() 时,PD的最大值为
时,PD的最大值为 ![]() ;
;

②过D作DG⊥x轴于点G,如图2,则DG∥OC
∴△BOC∽△BGD,
∴ ![]() ,
,
∵BD=2CD
∴BD:BC=2:3,
∴DG= ![]() OC=2,
OC=2,
∴点D的纵坐标为2,
把y=2代入y=﹣x+3得x=1,
∴D点坐标为(1,2),
设直线PD解析式为y=x+b
把D(1,2)代入上式得2=1+b,解得b=1
∴直线PD解析式为y=x+1,
解方程组 ![]() 得
得 ![]() 或
或 ![]() ,
,
∴P(2,3),
即当BD=2CD时,t的值为2;

(3)解:当四边形BQCM为平行四边形时,点Q向左平移1个单位可得到C点,则点B向左平移1个单位得到M点,
即M点的横坐标为2,当x=2时,y=﹣x2+2x+3=3,此时M点的坐标为(2,3);当四边形BCQM为平行四边形时,点C向右平移1个单位可得到Q点,则点B向右平移1个单位可得到M点,即M点的横坐标为4,当x=4时,y=﹣x2+2x+3=﹣5,此时M点的坐标为(4,﹣5);当四边形BCMQ为平行四边形时,点B向左平移2个单位可得到Q点,则点C向左平移2个单位得到M点,即M点的横坐标为﹣1,当x=﹣2时,y=﹣x2+2x+3=﹣5,此时M点的坐标为(﹣2,﹣5),
综上所述,满足条件的M点的坐标为(2,3),(4,﹣5),(﹣2,﹣5).
【解析】(1)利用待定系数法求抛物线解析式;(2)①过P作PN⊥x轴于点N,交BC于点E,如图1,先利用待定系数法求出直线BC解析式为y=﹣x+3,设点P的坐标为(t,﹣t2+2t+3),则E(t,﹣t+3),所以PE=﹣t2+3t,再判定△PDE为等腰直角三角形得到PD= ![]() PE,所以PD=
PE,所以PD= ![]() (﹣t2+3t),然后就利用二次函数的性质解决问题;②过D作DG⊥x轴于点G,如图2,通过证明△BOC∽△BGD,利用相似比可求出DG=2,则点D的纵坐标为2,于是利用二次函数解析式可确定D点坐标,接着求出直线PD解析式为y=x+1,然后解方程组
(﹣t2+3t),然后就利用二次函数的性质解决问题;②过D作DG⊥x轴于点G,如图2,通过证明△BOC∽△BGD,利用相似比可求出DG=2,则点D的纵坐标为2,于是利用二次函数解析式可确定D点坐标,接着求出直线PD解析式为y=x+1,然后解方程组 ![]() 可得到P点坐标,从而得到t的值;(3)讨论:当四边形BQCM为平行四边形或四边形BCQM为平行四边形或四边形BCMQ为平行四边形,然后利用平行四边形的性质和点的平移坐标规律确定M点的横坐标,再利用二次函数解析式确定M点的纵坐.
可得到P点坐标,从而得到t的值;(3)讨论:当四边形BQCM为平行四边形或四边形BCQM为平行四边形或四边形BCMQ为平行四边形,然后利用平行四边形的性质和点的平移坐标规律确定M点的横坐标,再利用二次函数解析式确定M点的纵坐.

 口算题天天练系列答案
口算题天天练系列答案