题目内容
【题目】△ABC中,∠BAC>90°,∠ACB=∠ABC=α,点D为BC边上任意一点,点E在AD延长线上,且BC=BE.
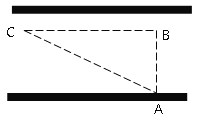
(1)当α=30°,点D恰好为BC中点时,补全图1,求∠BEA的度数;
(2)如图2,若∠BAE=2α,此时恰好DB=DE,连接CE,求证:△ABE≌△CEB.

【答案】(1)30°(2)证明见解析
【解析】
(1)只要证明AE⊥BC,△BCE是等边三角形即可解决问题;
(2)如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N,只要证明Rt△BMF≌Rt△BNE,推出∠BEA=∠F,由BF=BC,推出∠F=∠C=α,推出∠BEA=α即可.
(1)补全图1,如图所示.
∵AB=AC,BD=DC,
∴AE⊥BC,
∴EB=EC,∠ADB=90°,
∵∠ABC=30°,
∴∠BAE=60°
∵BC=BE,
∴△BCE是等边三角形,∠DEB=∠DEC,
∴∠BEA=30°;
(2)延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N,
∵∠ACB=∠ABC=α,
∴∠FAB=∠ABC+∠ACB=2α,
∵∠BAE=2α,
∴∠MAB=∠NAB,
∴BM=BN,
在Rt△BMF与Rt△BNE中,
![]() ,
,
∴Rt△BMF≌Rt△BNE(HL),
∴∠F=∠AEB,
∵BF=BC,
∴∠F=∠ACB=α,
∴∠AEB=α,
∴∠ACB=∠AEB,
∴A,B,E,C四点共圆,
∴∠BAE=∠ECB,
在△ABE与△CEB中,
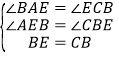 ,
,
∴ABE≌△CEB(AAS).

【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.