题目内容
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
【答案】
(1)解:由题意,设抛物线的解析式为y=a(x﹣4)2﹣ ![]() (a≠0)
(a≠0)
∵抛物线经过(0,2)
∴a(0﹣4)2﹣ ![]() =2
=2
解得:a= ![]()
∴y= ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]()
即:y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
当y=0时, ![]() x2﹣
x2﹣ ![]() x+2=0
x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0)
(2)解:存在,如图2,
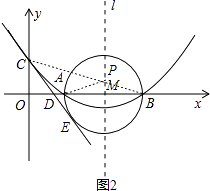
由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2 ![]() ,
,
∴AP+CP=BC=2 ![]()
∴AP+CP的最小值为2 ![]()
(3)解:如图3,连接ME
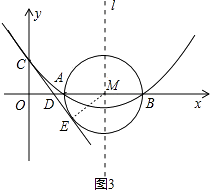
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
∵C的坐标(0,2),
∴OC=2,
∵AB=4,
∴ME=2
∴OC=ME=2,
∵∠ODC=∠MDE,
∵在△COD与△MED中
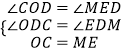
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
则CD=DM=OM﹣OD=4﹣x
则Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4﹣x)2
∴x= ![]()
∴D( ![]() ,0)
,0)
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D( ![]() ,0)两点,
,0)两点,
则 
解得: 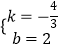
∴直线CE的解析式为y=﹣ ![]() +2;
+2;
【解析】(1)已知顶点坐标,因此函数解析式设成顶点式,再将点C的坐标代入即可求得函数解析式,由y=0,建立方程求解即可得到抛物线与x轴的两交点坐标。
(2)要在抛物线的对称轴l上求作点P,使AP+CP的值,抛物线是关于对称轴对称,点A关于直线l的对称点是点B,因此连接BC交直线l于点P,要求AP+CP的值,可证得AP+CP=BC,再Rt△OBC中根据勾股定理即可求出BC的长。
(3)由已知点A、B的坐标及AB时直径,可证得OC=ME,即可证明△COD≌△MED,得出OD=DE,DC=DM。运用勾股定理Rt△COD中,求出OD的长,即可求出点D的坐标,利用待定系数法,即可直线CE的解析式。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
【题目】某公司有某种海产品2104千克,寻求合适价格,进行8天试销,情况如下:
第几天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
销售价格(元/千克) | 400 | A | 250 | 240 | 200 | 150 | 125 | 120 |
销售量(千克) | 30 | 40 | 48 | B | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用某种函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系. 现假设这批海产品的销售中,每天销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1)猜想函数关系式: . (不必写出自变量的取值)并写出表格中A= ,B= ;
(2)试销8天后,公司决定将售价定为150元/千克. 则余下海产品预计 天可全部售出;
(3)按(2)中价格继续销售15天后,公司发现剩余海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新价格销售,那么新确定的价格最高不超过多少元/千克才能完成销售任务?






