题目内容
【题目】如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过点G作GE⊥AD于点E.若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFOC=![]() .其中正确的有( )
.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据“菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质和直角三角形的相关性质”结合“已知条件”进行分析解答即可.
(1)∵四边形ABCD是菱形,
∴∠FAG=∠EAG,∠1=∠GAD,AB=AD,
∵∠1=∠2,
∴∠GAD=∠2,
∴AG=GD,
∵GE⊥AD,
∴GE垂直平分AD,
∴AE=ED,
∵F为边AB的中点,
∴AF=AE,
在△AFG和△AEG中,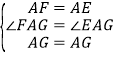 ,
,
∴△AFG≌△AEG(SAS),
∴∠AFG=∠AEG=90°,
∴DF⊥AB,故结论①正确;
(2)如图1,连接BD交AC于点O,
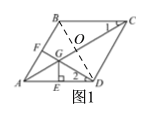
∵DF⊥AB,F为边AB的中点,
∴AF=![]() AB=1,AD=BD,
AB=1,AD=BD,
又∵菱形ABCD中,AB=AD,
∴AD=BD=AB,
∴△ABD为等边三角形,
∴∠BAD=∠BCD=60°,
∴∠BAC=∠1=∠2=30°,
∴AC=2AO=2ABcos∠BAC=2×2×![]() ,AG=
,AG=![]() ,
,
∴CG=AC-AG=![]() ,
,
∴CG=2GA,故②中结论正确;
(3)∵GE垂直平分AD,
∴ED=![]() AD=1,
AD=1,
∴GE=tan∠2ED=tan30°×1=![]() ,
,
∵在Rt△ADF中,AD=2,AF=1,
∴DF=![]() ,
,
∴DF+GE=![]() ,
,
又∵CG=![]() ,
,
∴CG=DF+GE,故③中结论正确;
(4)∵在Rt△AOB中,∠BAC=30°,∠BOA=90°,AB=2,
∴BO=![]() AB=1,
AB=1,
∵在Rt△AFG中,∠FAG=30°,∠GFA=90°,
∴FG=AF·tan30°=![]() ,
,
∴S四边形BFGC=S△ABC-S△AGF
=![]() AC·OB-
AC·OB-![]() AF·FG
AF·FG
=![]()
=![]() .
.
∴④中结论不正确;
综上所述,上述4个结论中正确的有3个.
故选:D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图是用长度相等的小棒按一定规律摆成的一组图案

(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.8千克时,t的值为( )
A. 128B. 132C. 136D. 140