题目内容
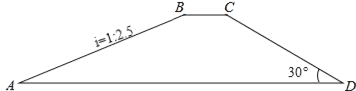
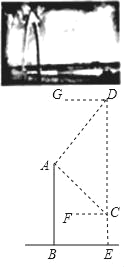
【题目】通达桥即小店汾河桥,是太原新建成的一座跨汾大桥,也是太原首座悬索桥.桥的主塔由曲线形拱门组成,取意“时代之门”.无人机社团的同学计划利用无人机设备测量通达桥拱门的高度.如图,他们先将无人机升至距离桥面50米高的点C处,测得桥的拱门最高点A的仰角∠ACF为30°,再将无人机从C处竖直向上升高200米到点D处,测得点A的俯角∠ADG为45°.已知点A,B,C,D,E在同一平面内,求通达桥拱门最高点A距离桥面BE的高度AB.(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】通达桥拱门最高点A距离桥面BE的高度AB约为123米.
【解析】
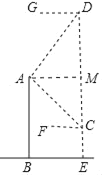
如图,作AM⊥DE于M.根据CD=200米,构建方程求出CM即可解决问题.
解:如图,作AM⊥DE于M.
∴∠AMD=∠AMC=90°,
在Rt△ACM中,∠ACM=90°﹣∠ACF=90°﹣30°=60°,
∴tan∠ACM=tan60°=![]() =
=![]() ,
,
∴AM=![]() CM,
CM,
在Rt△ADM中,∠ADM=90°﹣∠ADG=90°﹣45°=45°,
∴tan∠ADM=tan45°=![]() =1,
=1,
∴AM=DM=![]() CM,
CM,
由题意:CD=200米,
∴CM+![]() CM=200,
CM=200,
∴CM=![]() ≈73(米),
≈73(米),
∵∠ABE=∠AME=∠MEB=90°,
∴四边形ABEM是矩形,
∴AB=ME=MC+CE=73+50=123(米).
答:通达桥拱门最高点A距离桥面BE的高度AB约为123米.

练习册系列答案
相关题目