题目内容
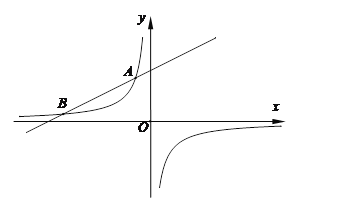
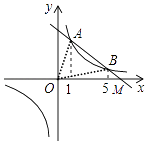
【题目】如图，直线y1=kx+b与双曲线y2= 
交于A、B两点，它们的横坐标分别为1和5． 
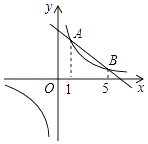
（1）当m=5时，求直线AB的解析式及△AOB的面积；
（2）当y1＞y2时，直接写出x的取值范围．
【答案】
（1）解：①当m=5时，
∴A（1，5），B（5，1），
设y=kx+b，代入A（1，5），B（5，1）得： 
，
解得： 
∴y=﹣x+6；
②设直线AB与x轴交点为M，
∴M（6，0），
∴SAOB=S△AOM﹣S△MOB= 
×6×5﹣ ×6×1=12
（2）解：由图象可知：1＜x＜5或x＜0．
【解析】（1）根据待定系数法即可求得直线AB的解析式，然后求得直线与x轴的交点，根据三角形面积公式求得即可．（2）根据图象求得即可．
练习册系列答案
阅读快车系列答案
相关题目
【题目】探究多边形内角和问题．
连接多边形不相邻的两个顶点的线段叫做多边形的对角线．从多边形某一个顶点出发的×对角线可以把一个多边形分成几个三角形．这样就把多边形内角和问题转化为三角形内角和问题了．
（1）请你试一试，做一做，把下面表格补充完整：
名称 | 图形 | 内角和 |
三角形 |
| 180° |
四边形 |
| 2×180°=360° |
五边形 |
|
|
六边形 |
|
|
… | … | … |
根据表格探究发现的规律，完成下面的问题：
（2）七边形的内角和等于 度；
（3）如果一个多边形有n条边，请你用含有n的代数式表示这个多边形的内角和： ．
