题目内容
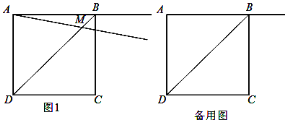
【题目】正方形ABCD的边长为2,过点A作射线AM与线段BD交于点M,∠BAM=α(0°<α<90°),作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.
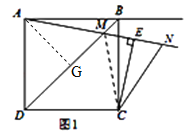
(1)如图①,当0°<α<45°时,
①依题意在图①中补全图并证明:AM=CN ②当BD∥CN,求DM的值
(2)探究∠NCE与∠BAM之间的数量关系并加以证明.
【答案】(1)①补图见解析,证明见解析;②![]() ;(2)①当0°<α<45°时,∠NCE=2∠BAM;②当45°<α<90°时,
;(2)①当0°<α<45°时,∠NCE=2∠BAM;②当45°<α<90°时,![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.
【解析】(1)①补全的图形即可.先证明△ABM≌△CBM得AM=MC,再根据点N与点M关于直线CE对称得CM=CN,即可得到结论;
②由平行线的性质得到∠AMD=∠ANC,又由等腰三角形的性质得到∠CMN=∠CNM,由①中△ABM≌△CBM得∠AMB=∠CMB,从而∠AMD=∠CMD,进一步得到∠CMN=∠AMD=∠CMD=60°,∠ADB=45°,过点A作AG⊥BD,根据边长为2,可以求出DM的长.
(2)分两种情况讨论:①当0°<α<45°时,∠NCE=2∠BAM.作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.由△ABM≌△CBM,可得∠BAM=∠BCM,由∠ABC=∠CEA=90°,BC,AE交于一点,可得∠BAM=∠BCE,即可得到∠MCE=2∠BAM,由点N与点M关于直线CE对称,可得CN=CM,即可得到∠NCE=∠MCE,进而得出∠NCE=2∠BAM.
②当45°<α<90°时,![]() .连接CM,判定△ADM≌△CDM,即可得到∠DAM=∠DCM,再根据∠DAQ=∠ECQ,即可得到∠NCE=∠MCE=2∠DAQ,即
.连接CM,判定△ADM≌△CDM,即可得到∠DAM=∠DCM,再根据∠DAQ=∠ECQ,即可得到∠NCE=∠MCE=2∠DAQ,即![]() ,再根据∠BAM=∠BCM,∠BCM+∠DCM=90°,即可得到
,再根据∠BAM=∠BCM,∠BCM+∠DCM=90°,即可得到![]() .
.
(1)①补全的图形如图所示.
∵ABCD是正方形,∴AB=BC,∠ABM=∠CBM,BM=BM,∴△ABM≌△CBM,∴AM=MC.
∵点N与点M关于直线CE对称,∴CM=CN,∴AM=CN;
②∵BD∥CN,∴∠AMD=∠ANC.
又∵CM=CN,∴∠CMN=∠CNM,由①中△ABM≌△CBM得∠AMB=∠CMB,∴∠AMD=∠CMD,∴∠CMN=∠AMD=∠CMD=60°,∠ADB=45°.
过点A作AG⊥BD.
∵AD=2,∠ADG=45°,∴AG=DG=![]() .
.
∵∠AMD=60°,∴∠MAG=30°,∴MG=![]() ,∴DM=
,∴DM=![]() .
.
(2)①当0°<α<45°时,NCE=2∠BAM.
如图1,连接MC,∵△ABM≌△CBM,∴∠BAM=∠BCM,∵∠ABC=∠CEA=90°,BC,AE交于一点,∴∠BAM=∠BCE,∴∠MCE=2∠BAM,由点N与点M关于直线CE对称,可得CN=CM,∴∠NCE=∠MCE,∴∠NCE=2∠BAM.
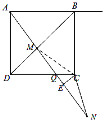
②当45°<α<90°时,![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.
如图,连接CM,∵AD=CD,∠ADM=∠CDM,DM=DM,∴△ADM≌△CDM,∴∠DAM=∠DCM.
∵∠ADQ=∠CEQ=90°,∠AQD=∠CQE,∴∠DAQ=∠ECQ,∴∠NCE=∠MCE=2∠DAQ,∴∠DCM=![]() ∠NCE.
∠NCE.
∵∠BAM=∠BCM,∠BCM+∠DCM=90°,∴![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案