题目内容
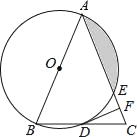
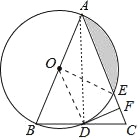
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.
【答案】(1)证明见解析;(2)S阴影= 16π﹣32.
【解析】试题分析:
(1)连接OD,AD,由AB是⊙O的直径可得∠ADB=90°,结合AB=AC可得点D是BC的中点,结合点O是AB中点可得OD是△ABC的中位线,由此可得OD∥AC,结合DF⊥AC即可得到DF⊥OD,由此可得DF是⊙O的切线;
(2)连接OE,由DF⊥AC于点F结合∠CDF=22.5°可得∠C=67.5°,这样结合AB=AC可得∠B=67.5°,从而可得∠BAC=45°,再结合AO=EO即可得到∠AOE=90°,这样就可由S阴影=S扇形AOE-S△AOE求出S阴影的大小了.
试题解析:
(1)连接OD,AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=AC,∠ADB=90°,
∴BD=CD,
∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴半径OD⊥DF,
∴DF是⊙O的切线.
(2)连接OE.
∵DF⊥AC,∠CDF=22.5°,
∴∠C=67.5°,
∵AB=AC,
∴∠C=∠B=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
又∵⊙O的半径为8,
∴S阴影=S扇形AOE﹣S△AOE=16π﹣32.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 (单位:克) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为450±5克,求该食品的抽样检测的合格率.