题目内容
【题目】已知抛物线y=x2﹣2bx+c
(1)若抛物线的顶点坐标为(2,﹣3),求b,c的值;
(2)若b+c=0,是否存在实数x,使得相应的y的值为1,请说明理由;
(3)若c=b+2且抛物线在﹣2≤x≤2上的最小值是﹣3,求b的值.
【答案】
(1)解:∵抛物线y=x2﹣2bx+c
∴a=1,
∵抛物线的顶点坐标为(2,﹣3),
∴y=(x﹣2)2﹣3,
∵y=(x﹣2)2﹣3=x2﹣4x+1,
∴b=2,c=1;
(2)解:由y=1得 x2﹣2bx+c=1,
∴x2﹣2bx+c﹣1=0
∵△=4b2+4b+4=(2b+1)2+3>0,
则存在两个实数,使得相应的y=1;
(3)解:由c=b+2,则抛物线可化为y=x2﹣2bx+b+2,其对称轴为x=b,
①当x=b≤﹣2时,则有抛物线在x=﹣2时取最小值为﹣3,此时
﹣3=(﹣2)2﹣2×(﹣2)b+b+2,解得b=﹣ ![]() ,不合题意;
,不合题意;
②当x=b≥2时,则有抛物线在x=2时取最小值为﹣3,此时
﹣3=22﹣2×2b+b+2,解得b=3,
③当﹣2<b<2时,则 ![]() =﹣3,化简得:b2﹣b﹣5=0,解得:
=﹣3,化简得:b2﹣b﹣5=0,解得:
b1= ![]() (不合题意,舍去),b2=
(不合题意,舍去),b2= ![]() .
.
综上:b=3或 ![]() .
.
【解析】(1)根据题意得到抛物线为y=(x﹣2)2﹣3,整理成一般式即可求得b,c的值;(2)令y=1,判断所得方程的判别式大于0即可求解;(3)求得函数的对称轴是x=b,然后分成b≤﹣2,﹣2<b<2和b≥2三种情况进行讨论,然后根据最小值是﹣3,即可解方程求解.
【考点精析】利用二次函数的性质和二次函数的最值对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.

【题目】在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表: 该班学生参加各项服务的频数、频率统计表:
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表,解答下列问题: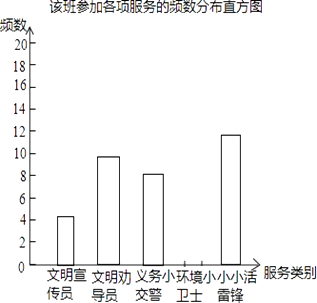
(1)该班参加这次公益活动的学生共有名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.