题目内容
【题目】我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一大重要研究成果．如图所示的三角形数表，称“杨辉三角”．具体法则：两侧的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律：
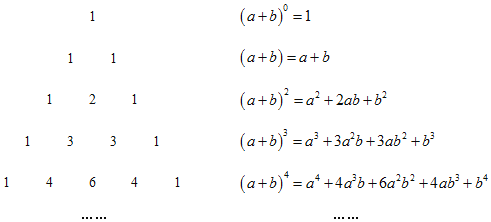
（1）根据上面的规律，写出（a+b）5的展开式；
（2）利用上面的规律计算：（﹣3）4+4×（﹣3）3×2+6×（﹣3）2×22+4×（﹣3）×23+24．
【答案】（1）（a+b）5＝a5+5a4b+10a3b2+10a2b3+5ab4+b5；（2）1.
【解析】
（1）根据上面的规律，按a的次数由大到小的顺序判断出各是多少，写出（a+b）5的展开式即可；
（2）利用上面的规律，（-3）4+4×（-3）3×2+6×（-3）2×22+4×（-3）×23+24=（-3+2）4，据此求出算式的值是多少即可．
解：（1）根据规律可得：（a+b）5首项a的次数是5次方，b为0次方，后续每项a的次数减少1而b的次数增加1，每项的系数根据规律则依次为为1，1+4=5，4+6=10，6+4=10，4+1=5，1，根据以上规律，则（a+b）5＝a5+5a4b+10a3b2+10a2b3+5ab4+b5；
（2）由题知：
，
对比（﹣3）4+4×（﹣3）3×2+6×（﹣3）2×22+4×（﹣3）×23+24
可知a=-3，b=2，
则原式＝（﹣3+2）4＝1.
练习册系列答案
相关题目
