题目内容
【题目】在平面直角坐标系中,点 A(a,6),B(4,b),
(1)若 a,b 满足 (a b 5)2 ![]() 0 ,
0 ,
①求点 A,B 的坐标;
②点 D 在第一象限,且点 D 在直线 AB 上,作 DC⊥x 轴于点 C,延长 DC 到 P 使 得 PC=DC,若△PAB 的面积为 10,求 P 点的坐标;
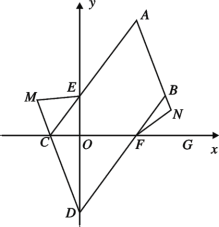
(2)如图,将线段 AB 平移到 CD,且点 C 在 x 轴负半轴上,点 D 在 y 轴负半轴上, 连接 AC 交 y 轴于点 E,连接 BD 交 x 轴于点 F,点 M 在 DC 延长线上,连 EM,3∠MEC+∠CEO=180°,点 N 在 AB 延长线上,点 G 在 OF 延长线上,∠NFG= 2∠NFB,请探究∠EMC 和∠BNF 的数量关系,给出结论并说明理由.
【答案】(1)①A(2,6),B(4,3).②P(![]() ,-5).(2)∠BNF-∠EMC=30°,理由见解析.
,-5).(2)∠BNF-∠EMC=30°,理由见解析.
【解析】
(1)①利用非负数的性质构建方程组解决问题即可.
②由题意AB的解析式为y=-![]() x+9,设D(m,-
x+9,设D(m,-![]() m+9),利用三角形的面积,构建方程解决问题即可.
m+9),利用三角形的面积,构建方程解决问题即可.
(2)结论:∠BNF-∠EMC=30°.设∠MEC=α,∠BFN=β,首先证明α-β=30°,再利用平行四边形的性质,三角形的外角的性质解决问题即可.
(1)①∵(a+b-5)2+|2a-b-1|=0,
又∵(a+b-5)2≥0,|2a-b-1|≥0,
∴![]() ,
,
∴![]() ,
,
∴A(2,6),B(4,3).
②如图1中,

∵A(2,6),B(4,3),
∴直线AB的解析式为y=-![]() x+9,设D(m,-
x+9,设D(m,-![]() m+9),
m+9),
∵CD=PC,
∴PD=-3m+18,
∵S△PAB=10,
∴![]() ×PD×2=10,
×PD×2=10,
∴-3m+18=10,
∴m=![]() ,
,
∴D(![]() ,5),
,5),
∴P(![]() ,-5).
,-5).
(2)结论:∠BNF-∠EMC=30°.
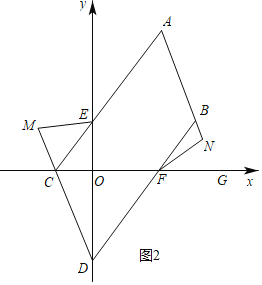
理由:设∠MEC=α,∠BFN=β,
∵3∠MEC+∠CEO=180°,∠AEO+∠CEO=180°,
∴∠AEO=3α,
∵∠NFG=2∠BFN,
∴∠NFG=2β,∠OFD=∠BFG=3β,
∵AB=CD,AB∥CD,
∴四边形ABDC是平行四边形,
∴AC∥BD,∠ACD=∠ABD,
∴∠BDE=180°-∠AEO=180°-3α,
∵∠BDE+∠OFD=90°,
∴180°-3α+3β=90°,
∴α-β=30°,
∵∠ACD=∠EMC+∠MEC,∠ABD=∠BFN+∠BNF,
∴∠EMC+α=∠BNF+β,
∴∠BNF-∠EMC=α-β=30°.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案