题目内容
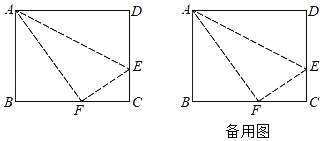
【题目】如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处
(1)求CE的长;
(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.
【答案】(1)3;(2)存在,![]() .
.
【解析】
(1)先判断出AF=AD=8,进而利用勾股定理求出BF=6,最后在Rt△ECF,利用勾股定理,即可得出结论;
(2)先作出点E关于BC的对称点E,进而求出DE',再利用勾股定理即可得出结论.
解:(1)长方形ABCD中,AB=8,BC=10,
∴∠B=∠BCD=90°,CD=AB=8,AD=BC=10,
由折叠知,EF=DE,AF=AD=8,
在Rt△ABF中,根据勾股定理得,BF=![]() =6,
=6,
∴CF=BC﹣BF=4,
设CE=x,则EF=DE=CD﹣CE=8﹣x,
在Rt△ECF中,根据勾股定理得,CF2+CE2=EF2,
∴16+x2=(8﹣x)2,
∴x=3,
∴CE=3;
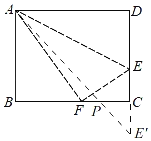
(2)如图,延长EC至E'使CE'=CE=3,连接AE'交BC于P,
此时,PA+PE最小,最小值为AE',
∵CD=8,
∴DE'=CD+CE'=8+3=11,
在Rt△ADE'中,根据勾股定理得,AE'=![]() =
=![]() .
.

练习册系列答案
相关题目