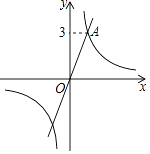Question

【题目】已知：如图，一次函数 与反比例函数 的图象在第一象限的交点为A（1，n）．

（1）求m与n的值；
（2）设一次函数的图象与x轴交于点B，连结OA，求∠BAO的度数．

Answer 1

【答案】
（1）解：∵点A（1，n）在双曲线 上，

∴n= ，

又∵A（1， ）在直线y= x+m上，

∴m=

（2）解：过点A作AM⊥x轴于点M．

∵直线 与x轴交于点B，

∴ ．

解得 x=﹣2．

∴点B的坐标为（﹣2，0）．

∴OB=2，

∵点A的坐标为 ，

∴AM= ，OM=1，

在Rt△AOM中，∠AMO=90°，

∴tan ，

∴∠AOM=60°，

由勾股定理，得 OA=2，

∴OA=OB，

∴∠OBA=∠BAO，

∴∠BAO= AOM=30°，

∴sin∠BAO= ，

∴∠BA0=30°．

【解析】（1）把点A（1，n）坐标代入 即可求得n，再把 坐标代入 可求m；（2）由直线 ，求得点B的坐标为（﹣2，0），即OB=2，由点A的坐标为 ，由三角函数可求得∠AOM=60°，由勾股定理求得得 OA=2，得到OA=OB，推出∠OBA=∠BAO，于是求得∠BAO=30°，由正弦函数的定义可得结论．