Question

【题目】设在一个变化过程中有两个变量x与y，如果对于x的每一个值，y都有唯一确定的值和它对应，那么就说y是x的函数，记作y=f（x）．在函数y=f（x）中，当自变量x=a时，相应的函数值y可以表示为f（a）．
例如：函数f（x）=x2﹣2x﹣3，当x=4时，f（4）=42﹣2×4﹣3=5在平面直角坐标系xOy中，对于函数的零点给出如下定义：
如果函数y=f（x）在a≤x≤b的范围内对应的图象是一条连续不断的曲线，并且f（a）．f（b）＜0，那么函数y=f（x）在a≤x≤b的范围内有零点，即存在c（a≤c≤b），使f（c）=0，则c叫做这个函数的零点，c也是方程f（x）=0在a≤x≤b范围内的根．
例如：二次函数f（x）=x2﹣2x﹣3的图象如图1所示．

观察可知：f（﹣2）＞0，f（1）＜0，则f（﹣2）．f（1）＜0．所以函数f（x）=x2﹣2x﹣3在﹣2≤x≤1范围内有零点．由于f（﹣1）=0，所以，﹣1是f（x）=x2﹣2x﹣3的零点，﹣1也是方程x2﹣2x﹣3=0的根．
（1）观察函数y1=f（x）的图象2，回答下列问题：
①f（a）f（b） 0（“＜”“＞”或“=”）
②在a≤x≤b范围内y1=f（x）的零点的个数是 ．
（2）已知函数y2=f（x）=﹣ 的零点为x1 ， x2 ， 且x1＜1＜x2 ．
①求零点为x1 ， x2（用a表示）；
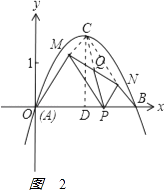
②在平面直角坐标xOy中，在x轴上A，B两点表示的数是零点x1 ， x2 ， 点 P为线段AB上的一个动点（P点与A、B两点不重合），在x轴上方作等边△APM和等边△BPN，记线段MN的中点为Q，若a是整数，求抛物线y2的表达式并直接写出线段PQ长的取值范围．

Answer 1

【答案】
（1）＜；1
（2）

解：①∵x1、x2是零点

∴当y=0时，即﹣ =0．

方程可化简为 x2+2（a﹣1）x+（a2﹣2a）=0．

解方程，得x=﹣a或x=﹣a+2．

∵x1＜1＜x2，﹣a＜﹣a+2，

∴x1=﹣a，x2=﹣a+2．

②∵x1＜1＜x2，

∴﹣a＜1＜﹣a+2．

∴﹣1＜a＜1．

∵a是整数，

∴a=0，所求抛物线的表达式为y=﹣ x2+2 ．

此时顶点C的坐标为C（1， ）如图2，

，

作CD⊥AB于D，连接CQ，

则AD=1，CD= ，tan∠BAC= ，

∴∠BAC=60°

由拋物线的对称性可知△ABC是等边三角形；

由△APM和△BPN是等边三角形，线段MN的中点为Q可得，

点M、N分别在AC和BC边上，四边形PMCN的平行四边形，

C、Q、P三点共线，且PQ= PC；

∵点P线段AB上运动的过程中，P与A、B两点不重合，

DC≤PC＜AC，DC= ，AC=2，

即 ≤PQ＜ ，

∴ ≤PQ＜1；

线段PQ的长的取值范围为： ≤PQ＜1

【解析】解：（1）①由图象1，得f（a）f（b）＜0，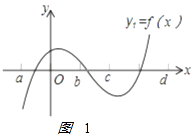

②在a≤x≤b范围内y1=f（x）的零点的个数是 1．
所以答案是：＜，1；