Question

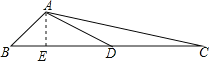
【题目】（1）如图，△ABC中，∠B=45°，AB=3 ，D是BC中点，tanC= ．求BC的长与sin∠ADB．

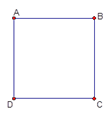
（2）如图，在平面直角坐标系中，点A（0，4），B（3，0），连接AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，求直线BC的解析式．

Answer 1

【答案】(1) sin∠ADB = ； (2) 直线BC的解析式为y=﹣x+．

【解析】试题分析：(1) 过A作AE⊥BC于E，根据三角形函数分别求出AE、BE、CE的长，从而得BC的长，再由点D为BC中点即可得到DE的长， 根据勾股定理得AD长，从而得到∠ADB人正弦；

（2）在Rt△OAB中，OA=4，OB=3，用勾股定理计算出AB=5，再根据折叠的性质得BA′=BA=5，CA′=CA，则OA′=BA′-OB=2，设OC=t，则CA=CA′=4-t，在Rt△OA′C中，根据勾股定理得到求得t的值，从而确定出点C坐标，然后利用待定系数法确定直线BC的解析式．

试题解析：(1) 过A作AE⊥BC于E， ∴∠AEB=90°，

∵∠B=45°，∵sinB= ，∴AE=ABsinB=3×=3，∴BE=AE=3，

∵∠AEC=90°，tanC= ，∴CE=15，∴BC=BE+CE=18；

∵D是BC中点，∴BD= BC=9，∴DE=BD﹣BE=6，

∴AD= =3 ， ∴sin∠ADB= = = ；

(2)∵A（0，4），B（3，0），∴OA=4，OB=3，

在Rt△OAB中，AB= =5,

∵△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，

∴BA′=BA=5，CA′=CA，∴OA′=BA′﹣OB=5﹣3=2,

设OC=t，则CA=CA′=4﹣t，在Rt△OA′C中，∵OC2+OA′2=CA′2，

∴t2+22=（4﹣t）2，解得t= ，∴C点坐标为（0， ），

设直线BC的解析式为y=kx+b，把B（3，0）、C（0， ）代入得 ，解得 ，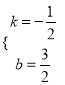

∴直线BC的解析式为y=﹣x+．