Question

【题目】综合题。
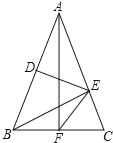
（1）如图1，已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°，求AD的长．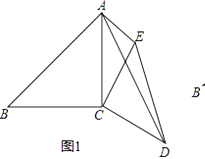
（2）如图2，已知∠ACB=∠DCE=90°，∠ABC=∠CED=∠CAE=30°，AC=3，AE=8，求AD的长．

Answer 1

【答案】
（1）解：如图1，连接BE，

∵∠ACB=∠DCE=90°，

∴∠ACB+∠ACE=∠DCE+∠ACE，即∠BCE=∠ACD，

又∵AC=BC，DC=EC，

在△ACD和△BCE中，

，

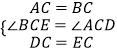∴△ACD≌△BCE，

∴AD=BE，

∵AC=BC=6，

∴AB=6 ，

∵∠BAC=∠CAE=45°，

∴∠BAE=90°，

在Rt△BAE中，AB=6 ，AE=3，

∴BE=9，

∴AD=9；

（2）解：如图2，连接BE，

在Rt△ACB中，∠ABC=∠CED=30°，

tan30°= = ，

∵∠ACB=∠DCE=90°，

∴∠BCE=∠ACD，

∴△ACD∽△BCE，

∴ = = ，

∵∠BAC=60°，∠CAE=30°，

∴∠BAE=90°，又AB=6，AE=8，

∴BE=10，

∴AD= ．

【解析】（1）连接BE，证明△ACD≌△BCE，得到AD=BE，在Rt△BAE中，AB=6 ，AE=3，求出BE，得到答案；（2）连接BE，证明△ACD∽△BCE，得到 = = ，求出BE的长，得到AD的长．
【考点精析】关于本题考查的勾股定理的概念和相似三角形的判定与性质，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．