题目内容
【题目】设一次函数y=kx+2k-3(k≠0),对于任意两个k的值k1,k2,分别对应两个一次函数值y1,y2,若k1k2<0,当x=m时,取相应y1,y2,中的较小值p,则p的最大值是________.
【答案】-3
【解析】
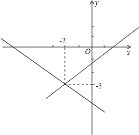
整理一次函数解析式求出不论k取任何值时一次函数经过的定点,再根据k1k2<0,可知两直线一条经过第一、三象限,一条经过第二、四象限，结合图象，当m=-2，相应的y1，y2中的较小值p，p最大值为-3．
解：如图，∵y=kx+2k+3=k（x+2）-3，
∴不论k取何值，当x=-2时，y=-3，
∴一次函数y=kx+2k-3经过定点（-2，-3），
又∵对于任意两个k的值k1、k2，k1k2＜0，
∴两个一次函数y1，y2，一个函数图象经过第一、三象限，一个经过第二、四象限，
∴当m=-2，相应的y1，y2中的较小值p，p最大值为-3．
故答案为：-3
练习册系列答案
一线名师提优试卷系列答案
相关题目
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，从该地区随机抽取部分七年级学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名同学只能选择其中一类节目），并调查得到的数据用下面的表和扇形图来表示（表、图都没制作完成）
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 36 | 90 | a | b | 27 |
根据表、图提供的信息，解决以下问题：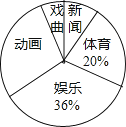
（1）计算出表中a、b的值；
（2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；
（3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？
