题目内容
【题目】如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB=15，AC=9，BC=12，阴影部分是△ABC的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（ ）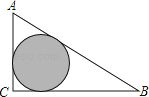 
A.
B.
C.
D.
【答案】B
【解析】解：∵AB=15，BC=12，AC=9，
∴AB2=BC2+AC2 ，
∴△ABC为直角三角形，
∴△ABC的内切圆半径= 
=3，∴S△ABC= 
ACBC= ×12×9=54，
S圆=9π，
∴小鸟落在花圃上的概率= 
= 
，
故选B．
【考点精析】本题主要考查了勾股定理的逆定理和三角形的内切圆与内心的相关知识点，需要掌握如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形；三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，从该地区随机抽取部分七年级学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名同学只能选择其中一类节目），并调查得到的数据用下面的表和扇形图来表示（表、图都没制作完成）
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 36 | 90 | a | b | 27 |
根据表、图提供的信息，解决以下问题：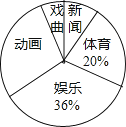
（1）计算出表中a、b的值；
（2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；
（3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？
