题目内容
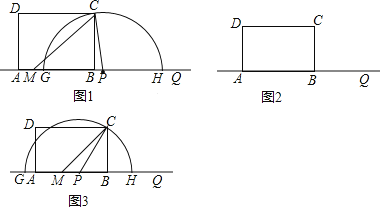
【题目】如图,在矩形ABCD中,AB=4,BC=3.点M是AB边上一点,且∠CMB=45°.点Q是直线AB上一点且在点B的右侧,BQ=4,点P从点Q出发,沿射线QA方向以每秒2个单位长度的速度运动,设运动时间为t秒.以P为圆心,PC长为半径作半圆P,交直线AB分别于点G,H(点G在点H的左侧).
(1)当t=1秒时,PC的长为 ,t= 秒时,半圆P与AD相切;
(2)当点P与点B重合时,求半圆P被矩形ABCD的对角线AC所截得的弦长;
(3)若∠MCP=15°,请直接写出扇形HPC的弧长为 .
【答案】(1)![]() ;
;![]() ; (2)
; (2)![]() ; (3)
; (3)![]() π或π.
π或π.
【解析】
(1)由点P的运动速度可找出t=1秒时PQ的长,进而可得出BP的长,在Rt△BCP中,利用勾股定理可求出PC的长;设当半圆P与AD相切时,BP=x,则PC=PA=4-x,利用勾股定理可得出关于x的方程,解之即可得出x的值,再结合PQ=BQ+BP即可求出此时t的值;
(2)过点B作BE⊥AC于点E,利用面积法可求出BE的长,在Rt△BCE中利用勾股定理可求出CE的长,再利用垂径定理可求出半圆P被矩形ABCD的对角线AC所截得的弦长;
(3)分点P在点M的左侧和点P在点M的右侧两种情况考虑:①当点P在点M的右侧时,∠CPB=60°,通过解直角三角形可求出PC的长,再利用弧长公式得到结论;②当点P在点M的左侧时,∠CPB=30°,通过解直角三角形可求出PC的长,再再利用弧长公式得到结论.
(1)当t=1秒时,PQ=2,
∴BP=BQ-PQ=2,
在Rt△BCP中,BP=2,BC=3,
∴PC=![]() ,
,
设当半圆P与AD相切时,BP=x,则PC=PA=4-x,
∴x2+32=(4-x)2,
解得:x=![]() ,
,
∴PQ=4+![]() =
=![]() ,
,
∴当t=![]() 时,半圆P与AD相切;
时,半圆P与AD相切;
故答案为:![]() ;
;![]() ;
;
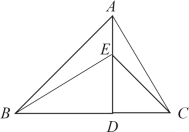
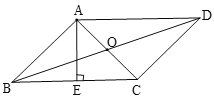
(2)过点B作BE⊥AC于点E,如图2所示.
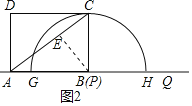
∵AB=4,BC=3,
∴AC=![]() =5,
=5,
∴BE=![]() .
.
在Rt△BCE中,BC=3,BE=![]() ,
,
∴CE=![]() ,
,
∴半圆P被矩形ABCD的对角线AC所截得的弦长为![]() ;
;
(3)分两种情况考虑,如图3所示:
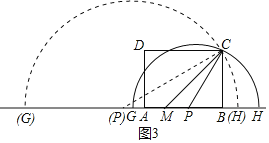
①当点P在点M的右侧时,∵∠CMB=45°,∠MCP=15°,
∴∠MCB=45°,∠PCB=30°,
∴∠CPB=60°,CP=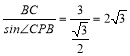 ,
,
∴扇形HPC的弧长为![]() π;
π;
②当点P在点M的左侧时,∵∠MCB=45°,∠MCP=15°,
∴∠PCB=∠MCB+∠MCP=60°,
∴∠CPB=30°,CP=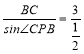 =6,
=6,
∴扇形HPC的弧长为![]() =π,
=π,
综上所述,若∠MCP=15°,扇形HPC的弧长为![]() π或π,
π或π,
故答案为:![]() π或π.
π或π.